Ранг на матрицата накратко. Определяне на ранга на матрица

Всякаква матрица Апоръчка m×nможе да се разглежда като колекция мнизови вектори или нколонни вектори.

Рангматрици Апоръчка m×nе максималният брой линейно независими вектори в колони или вектори в редове.

Ако рангът на матрицата Аравно на r, тогава е написано:

Намиране на ранга на матрица

Позволявам Аматрица на произволен ред м× н. Да се ​​намери рангът на матрица АКъм него прилагаме метода на елиминиране на Гаус.

Обърнете внимание, че ако на някакъв етап от елиминирането водещият елемент е равен на нула, тогава разменяме този ред с реда, в който водещият елемент е различен от нула. Ако се окаже, че няма такъв ред, преминете към следващата колона и т.н.

След процеса на Гаусово елиминиране, ние получаваме матрица, чиито елементи под главния диагонал са равни на нула. Освен това може да има вектори с нулев ред.

Броят на ненулевите редови вектори ще бъде рангът на матрицата А.

Нека да разгледаме всичко това с прости примери.

Пример 1.

Умножавайки първия ред по 4 и добавяйки към втория ред и умножавайки първия ред по 2 и добавяйки към третия ред, имаме:

Умножете втория ред по -1 и го добавете към третия ред:

Получихме два ненулеви реда и следователно рангът на матрицата е 2.

Пример 2.

Нека намерим ранга на следната матрица:

Умножете първия ред по -2 и го добавете към втория ред. По същия начин нулираме елементите на третия и четвъртия ред на първата колона:

Нека нулираме елементите на третия и четвъртия ред на втората колона, като добавим съответните редове към втория ред, умножени по числото -1.

Ще разгледаме и важно практическо приложение на темата: изследване на система от линейни уравнения за съгласуваност.

Какъв е рангът на една матрица?

Хумористичният епиграф на статията съдържа голяма доза истина. Обикновено свързваме думата „ранг“ с някаква йерархия, най-често с кариерна стълба. Колкото повече знания, опит, способности, връзки и т.н. – толкова по-висока е неговата позиция и набор от възможности. По отношение на младежта рангът се отнася до общата степен на „стръмнина“.

И нашите математически братя живеят по същите принципи. Нека вземем няколко случайни на разходка нулеви матрици:

Нека помислим за това, ако в матрицата всички нули, тогава за какъв ранг можем да говорим? Всеки е запознат с неофициалния израз „пълна нула“. В обществото на матриците всичко е абсолютно същото:

Ранг на нулевата матрицавсеки размер е равен на нула.

Забележка : Нулевата матрица се обозначава с гръцката буква "тета"

За да разбера по-добре ранга на матрицата, по-нататък ще използвам помощни материали аналитична геометрия. Помислете за нула векторнашето триизмерно пространство, което не задава конкретна посока и е безполезно за изграждане афинна основа. От алгебрична гледна точка координатите на този вектор са записани в матрица„едно по три“ и логично (в посочения геометричен смисъл)приемем, че рангът на тази матрица е нула.

Сега нека разгледаме няколко ненулев колонни векториИ редови вектори:


Всеки екземпляр има поне един ненулев елемент и това е нещо!

Рангът на всеки ненулев вектор на ред (вектор на колона) е равен на единица

И най-общо казано - ако в матрицата произволни размериима поне един ненулев елемент, тогава неговият ранг не по-малкоединици.

Алгебричните редови вектори и колонните вектори са до известна степен абстрактни, така че нека се обърнем отново към геометричната асоциация. Не-нула векторзадава много категорична посока в пространството и е подходящ за изграждане основа, следователно рангът на матрицата ще се счита за равен на единица.

Теоретична информация : в линейната алгебра векторът е елемент от векторно пространство (дефинирано чрез 8 аксиоми), което по-специално може да представлява подреден ред (или колона) от реални числа с дефинирани операции събиране и умножение с реално число за тях. По-подробна информация за векторите можете да намерите в статията Линейни трансформации.

линейно зависими(изразени един през друг). От геометрична гледна точка вторият ред съдържа координатите на колинеарния вектор , което изобщо не придвижи въпроса в строителството триизмерна основа, бидейки в този смисъл излишен. По този начин рангът на тази матрица също е равен на единица.

Нека пренапишем координатите на векторите в колони ( транспониране на матрицата):

Какво се промени по отношение на ранга? Нищо. Колоните са пропорционални, което означава, че рангът е равен на единица. Между другото, имайте предвид, че и трите линии също са пропорционални. Те могат да бъдат идентифицирани с координатите триколинеарни вектори на равнината, от които само единполезно за изграждане на "плоска" основа. И това е напълно в съответствие с нашето геометрично чувство за ранг.

Важно твърдение следва от горния пример:

Рангът на матрицата в редове е равен на ранга на матрицата в колони. Вече споменах това малко в урока за ефективното методи за изчисляване на детерминанта.

Забележка : линейната зависимост на редовете предполага линейна зависимост на колоните (и обратно). Но за да спестя време и по навик, почти винаги ще говоря за линейна зависимост на низовете.

Нека продължим да обучаваме нашия любим домашен любимец. Нека добавим координатите на друг колинеарен вектор към матрицата в третия ред :

Той помогна ли ни в изграждането на триизмерна основа? Разбира се, че не. И трите вектора вървят напред-назад по един и същ път, а рангът на матрицата е равен на единица. Можете да вземете колкото искате колинеарни вектори, да речем 100, да поставите координатите им в матрица „сто на три“ и рангът на такъв небостъргач пак ще остане един.

Нека се запознаем с матрицата, чиито редове линейно независими. Двойка неколинеарни вектори е подходяща за конструиране на триизмерна основа. Рангът на тази матрица е две.

Какъв е рангът на матрицата? Линиите не изглеждат пропорционални... така че на теория те са три. Рангът на тази матрица обаче също е два. Добавих първите два реда и отдолу написах резултата, т.е. линейно изразенотретия ред през първите два. Геометрично редовете на матрицата съответстват на координатите на три копланарни вектори, и сред тези три има двойка неколинеарни другари.

Както виждаш, линейна зависимоств разглежданата матрица не е очевидно и днес ще научим как да го изведем наяве.

Мисля, че много хора могат да познаят какъв е рангът на една матрица!

Да разгледаме матрица, чиито редове линейно независими. Векторна форма афинна основа, а рангът на тази матрица е три.

Както знаете, всеки четвърти, пети, десети вектор на триизмерното пространство ще бъде линейно изразен чрез базисни вектори. Следователно, ако добавите произволен брой редове към матрица, тогава нейният ранг пак ще бъде равно на три.

Подобни разсъждения могат да бъдат проведени за матрици с по-големи размери (разбира се, без никакво геометрично значение).

Определение : Рангът на матрицата е максималният брой линейно независими редове. Или: Рангът на матрицата е максималният брой линейно независими колони. Да, броят им винаги е един и същ.

Важна практическа насока също следва от горното: рангът на матрицата не надвишава нейния минимален размер. Например в матрицата четири реда и пет колони. Минималното измерение е четири, следователно рангът на тази матрица със сигурност няма да надвишава 4.

Наименования: в световната теория и практика няма общоприет стандарт за обозначаване на ранга на матрицата, най-често можете да срещнете: - както се казва, англичанинът пише едно, германецът - друго; Затова, въз основа на известния виц за американския и руски ад, нека обозначим ранга на матрицата с родна дума. Например: . И ако матрицата е „неназована“, от които има много, тогава можете просто да напишете .

Как да намерим ранга на матрица, използвайки второстепенни?

Ако баба ми имаше пета колона в нейната матрица, тогава тя трябваше да изчисли друг минор от 4-ти ред („синьо“, „малина“ + 5-та колона).

Заключение: максималният ред на ненулев минор е три, което означава .

Може би не всеки е разбрал напълно тази фраза: минор от 4-ти ред е равен на нула, но сред минорите от 3-ти ред имаше ненулев - следователно максималният ред ненулеввторостепенно и е равно на три.

Възниква въпросът, защо веднага не изчислим детерминантата? Е, първо, в повечето задачи матрицата не е квадратна, и второ, дори ако получите ненулева стойност, задачата най-вероятно ще бъде отхвърлена, тъй като обикновено включва стандартно решение „отдолу нагоре“. И в разглеждания пример нулевият детерминант от 4-ти ред ни позволява да заявим, че рангът на матрицата е само по-малък от четири.

Трябва да призная, че самият аз измислих проблема, който анализирах, за да обясня по-добре метода за граничене на непълнолетни. В реалната практика всичко е по-просто:

Пример 2

Намерете ранга на матрица, като използвате метода на второстепенните ребра

Решението и отговорът са в края на урока.

Кога алгоритъмът работи най-бързо? Нека се върнем към същата матрица четири на четири. . Очевидно решението ще бъде най-кратко в случай на „добро“ ъгъл непълнолетни:

И ако , то , в противен случай – .

Мисленето не е никак хипотетично - има много примери, когато цялата материя се ограничава само до ъглови минори.

В някои случаи обаче друг метод е по-ефективен и за предпочитане:

Как да намерим ранга на матрица с помощта на метода на Гаус?

Параграфът е предназначен за читатели, които вече са запознати с Метод на Гауси повече или по-малко се докопаха до него.

От техническа гледна точка методът не е нов:

1) използвайки елементарни трансформации, намаляваме матрицата до поетапна форма;

2) рангът на матрицата е равен на броя на редовете.

Това е абсолютно ясно използването на метода на Гаус не променя ранга на матрицата, а същността тук е изключително проста: според алгоритъма, по време на елементарни трансформации, всички ненужни пропорционални (линейно зависими) редове се идентифицират и премахват, което води до „сух остатък“ - максималният брой линейно независими редове.

Нека трансформираме старата позната матрица с координатите на три колинеарни вектора:

(1) Първият ред беше добавен към втория ред, умножен по –2. Първият ред беше добавен към третия ред.

(2) Нулевите линии се премахват.

Така остава един ред, следователно . Излишно е да казвам, че това е много по-бързо от изчисляването на девет нулеви минори от 2-ри ред и едва след това да се направи заключение.

Напомням ви, че само по себе си алгебрична матрицанищо не може да се променя, а трансформациите се извършват само с цел определяне на ранга! Между другото, нека се спрем още веднъж на въпроса защо не? Матрица на източника 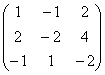носи информация, която е коренно различна от информацията на матрицата и реда. В някои математически модели (без преувеличение) разликата в едно число може да бъде въпрос на живот и смърт. ...Сетих се за начални и гимназиални учители по математика, които безмилостно намаляваха оценките с по 1-2 точки за най-малката неточност или отклонение от алгоритъма. И беше ужасно разочароващо, когато вместо привидно гарантирано „А“ се оказа „добро“ или дори по-лошо. Разбирането дойде много по-късно - как иначе да поверите сателити, ядрени бойни глави и електроцентрали на човек? Но не се притеснявайте, аз не работя в тези области =)

Нека да преминем към по-смислените задачи, където освен всичко друго ще се запознаем и с важни изчислителни техники Метод на Гаус:

Пример 3

Намерете ранга на матрица с помощта на елементарни трансформации

Решение: дадена е матрица „четири по пет“, което означава, че нейният ранг със сигурност е не повече от 4.

В първата колона няма 1 или –1, следователно са необходими допълнителни действия за получаване на поне една единица. По време на съществуването на сайта многократно ми е задаван въпросът: „Възможно ли е пренареждане на колони по време на елементарни трансформации?“ Ето, пренаредихме първата и втората колона и всичко е наред! В повечето задачи, където се използва Метод на Гаус, колоните наистина могат да се пренареждат. НО НЕ Е НУЖНО. И въпросът дори не е в възможно объркване с променливи, въпросът е, че в класическия курс на висшата математика това действие традиционно не се разглежда, така че такова кимване ще бъде разгледано МНОГО криво (или дори принудено да преработи всичко).

Втората точка се отнася до числата. Когато вземате решение, е полезно да използвате следното основно правило: елементарните трансформации трябва, ако е възможно, да намалят числата на матрицата. В крайна сметка е много по-лесно да работите с едно, две, три, отколкото например с 23, 45 и 97. И първото действие е насочено не само към получаване на единица в първата колона, но и към елиминиране на числата 7 и 11.

Първо пълното решение, след това коментари:

(1) Първият ред беше добавен към втория ред, умножен по –2. Първият ред беше добавен към третия ред, умножен по –3. И към купчината: 1-вият ред беше добавен към 4-тия ред, умножен по -1.

(2) Последните три реда са пропорционални. 3-ти и 4-ти ред бяха премахнати, вторият ред беше преместен на първо място.

(3) Първият ред беше добавен към втория ред, умножен по –3.

Редуцираната до ешелонна форма матрица има два реда.

Отговор:

Сега е ваш ред да измъчвате матрицата четири на четири:

Пример 4

Намерете ранга на матрица, като използвате метода на Гаус

Напомням ви това Метод на Гаусне предполага недвусмислена твърдост и вашето решение най-вероятно ще се различава от моето. Кратка примерна задача в края на урока.

Кой метод трябва да използвам, за да намеря ранга на матрица?

На практика често изобщо не се посочва кой метод трябва да се използва за намиране на ранга. В такава ситуация трябва да се анализира условието - за някои матрици е по-рационално да се решават чрез второстепенни, докато за други е много по-изгодно да се прилагат елементарни трансформации:

Пример 5

Намерете ранга на матрица

Решение: първият метод някак веднага изчезва =)

Малко по-високо посъветвах да не докосвате колоните на матрицата, но когато има нулева колона или пропорционални/съвпадащи колони, тогава все още си струва да ампутирате:

(1) Петата колона е нула, премахнете я от матрицата. По този начин рангът на матрицата е не повече от четири. Първият ред беше умножен по –1. Това е друга отличителна черта на метода на Гаус, която превръща следното действие в приятна разходка:

(2) Към всички редове, започвайки от втория, беше добавен първият ред.

(3) Първият ред беше умножен по –1, третият ред беше разделен на 2, четвъртият ред беше разделен на 3. Вторият ред беше добавен към петия ред, умножен по –1.

(4) Третият ред беше добавен към петия ред, умножен по –2.

(5) Последните два реда са пропорционални, петият се заличава.

Резултатът е 4 реда.

Отговор:

Стандартна пететажна сграда за самостоятелно обучение:

Пример 6

Намерете ранга на матрица

Кратко решение и отговор в края на урока.

Трябва да се отбележи, че фразата „ранг на матрицата“ не се среща толкова често на практика и в повечето проблеми можете да се справите напълно без нея. Но има една задача, в която въпросната концепция е главният герой и ние ще завършим статията с това практическо приложение:

Как да изследваме система от линейни уравнения за последователност?

Често, в допълнение към решението системи от линейни уравненияспоред условието първо трябва да се изследва за съвместимост, тоест да се докаже, че изобщо съществува някакво решение. Ключова роля в такава проверка играе Теорема на Кронекер-Капели, което ще формулирам в необходимата форма:

Ако ранг системни матрициравен на ранг разширена матрична система, тогава системата е последователна и ако това число съвпада с броя на неизвестните, то решението е уникално.

По този начин, за да се изследва системата за съвместимост, е необходимо да се провери равенството , Където - системна матрица(запомнете терминологията от урока Метод на Гаус), А - разширена системна матрица(т.е. матрица с коефициенти на променливи + колона от свободни членове).

За да работим с концепцията за ранг на матрицата, ще ни е необходима информация от темата "Алгебрични допълнения и минори. Видове минори и алгебрични допълнения." На първо място, това се отнася до термина „минорна матрица“, тъй като ние ще определим ранга на матрицата точно чрез непълнолетните.

Ранг на матрицатае максималният ред на неговите второстепенни, сред които има поне един, който не е равен на нула.

Еквивалентни матрици- матрици, чиито рангове са еднакви помежду си.

Нека обясним по-подробно. Да предположим, че сред минори от втори ред има поне един, който е различен от нула. И всички малки, чийто ред е по-висок от две, са равни на нула. Заключение: рангът на матрицата е 2 Или, например, сред второстепенните от десети ред има поне един, който не е равен на нула. И всички минори, чийто ред е по-висок от 10, са равни на нула. Заключение: рангът на матрицата е 10.

Рангът на матрицата $A$ се означава по следния начин: $\rang A$ или $r(A)$. Рангът на нулевата матрица $O$ се приема за нула, $\rang O=0$. Позволете ми да ви напомня, че за да образувате матричен минор, трябва да зачеркнете редове и колони, но е невъзможно да зачеркнете повече редове и колони, отколкото съдържа самата матрица. Например, ако матрицата $F$ има размер $5\times 4$ (т.е. съдържа 5 реда и 4 колони), тогава максималният ред на нейните минори е четири. Вече няма да е възможно да се формират второстепенни от пети ред, тъй като те ще изискват 5 колони (а ние имаме само 4). Това означава, че рангът на матрицата $F$ не може да бъде повече от четири, т.е. $\ранг F≤4$.

В по-обща форма горното означава, че ако една матрица съдържа $m$ реда и $n$ колони, тогава нейният ранг не може да надвишава най-малкия от $m$ и $n$, т.е. $\rang A≤\min(m,n)$.

По принцип от самата дефиниция на ранг следва методът за намирането му. Процесът на намиране на ранга на матрица, по дефиниция, може да бъде представен схематично, както следва:

Нека обясня тази диаграма по-подробно. Нека започнем да разсъждаваме от самото начало, т.е. от минори от първи ред на някаква матрица $A$.

1. Ако всички второстепенни елементи от първи ред (т.е. елементи на матрицата $A$) са равни на нула, тогава $\rang A=0$. Ако сред минорите от първи ред има поне един, който не е равен на нула, тогава $\rang A≥ 1$. Нека да преминем към проверка на непълнолетни от втори ред.
2. Ако всички минори от втори ред са равни на нула, тогава $\rang A=1$. Ако сред минори от втори ред има поне един, който не е равен на нула, тогава $\rang A≥ 2$. Да преминем към проверка на непълнолетни от трети ред.
3. Ако всички минори от трети ред са равни на нула, тогава $\rang A=2$. Ако сред минори от трети ред има поне един, който не е равен на нула, тогава $\rang A≥ 3$. Да преминем към проверката на непълнолетните от четвърти ред.
4. Ако всички минори от четвърти ред са равни на нула, тогава $\rang A=3$. Ако сред минори от четвърти ред има поне един, който не е равен на нула, тогава $\rang A≥ 4$. Преминаваме към проверка на малолетни от пети ред и т.н.

Какво ни очаква в края на тази процедура? Възможно е сред минори от k-ти порядък да има поне един, който е различен от нула, и всички (k+1) минори от порядък да бъдат равни на нула. Това означава, че k е максималният ред от второстепенни, сред които има поне един, който не е равен на нула, т.е. рангът ще бъде равен на k. Може да има различна ситуация: сред минори от k-ти ред ще има поне един, който не е равен на нула, но вече няма да е възможно да се формират (k+1) минори от ред. В този случай рангът на матрицата също е равен на k. Накратко, редът на последния съставен ненулев минор ще бъде равен на ранга на матрицата.

Нека да преминем към примери, в които процесът на намиране на ранга на матрица, по дефиниция, ще бъде ясно илюстриран. Позволете ми да подчертая още веднъж, че в примерите от тази тема ще започнем да намираме ранга на матриците, като използваме само определението за ранг. Други методи (изчисляване на ранга на матрица, използвайки метода на граничещи второстепенни, изчисляване на ранга на матрица, използвайки метода на елементарните трансформации) се обсъждат в следващите теми.

Между другото, изобщо не е необходимо да стартирате процедурата за намиране на ранга с непълнолетни от най-малък ред, както беше направено в примери № 1 и № 2. Веднага можете да преминете към второстепенни от по-високи степени (вижте пример № 3).

Пример №1

Намерете ранга на матрицата $A=\left(\begin(array)(ccccc) 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end(array) \right)$.

Тази матрица е с размер $3\пъти 5$, т.е. съдържа три реда и пет колони. От числата 3 и 5 минимумът е 3, следователно рангът на матрицата $A$ е не повече от 3, т.е. $\rang A≤ 3$. И това неравенство е очевидно, тъй като вече няма да можем да образуваме второстепенни от четвърти ред - те изискват 4 реда, а ние имаме само 3. Нека да преминем директно към процеса на намиране на ранга на дадена матрица.

Сред минори от първи ред (т.е. сред елементите на матрицата $A$) има ненулеви. Например 5, -3, 2, 7. По принцип не се интересуваме от общия брой на ненулевите елементи. Има поне един ненулев елемент - и това е достатъчно. Тъй като сред минорите от първи ред има поне един различен от нула, заключаваме, че $\rang A≥ 1$ и преминаваме към проверка на минорите от втори ред.

Нека започнем да изследваме второстепенни лица от втори ред. Например, в пресечната точка на редове № 1, № 2 и колони № 1, № 4 има елементи от следния минор: $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|. За тази детерминанта всички елементи от втората колона са равни на нула, следователно самата детерминанта е равна на нула, т.е. $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=0$ (вижте свойство № 3 в темата за свойствата на детерминантите). Или можете просто да изчислите този детерминант, като използвате формула № 1 от раздела за изчисляване на детерминанти от втори и трети ред:

$$ \left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=5\cdot 0-0\cdot 7=0. $$

Първият минор от втори ред, който тествахме, се оказа равен на нула. Какво означава това? Относно необходимостта от допълнителна проверка на непълнолетните от втори ред. Или всички те ще се окажат нула (и тогава рангът ще бъде равен на 1), или сред тях ще има поне един минор, който е различен от нула. Нека се опитаме да направим по-добър избор, като напишем минор от втори ред, чиито елементи са разположени в пресечната точка на редове № 1, № 2 и колони № 1 и № 5: $\left|\begin( array)(cc) 5 & 2 \\ 7 & 3 \end(array) \right|$. Нека намерим стойността на този минор от втори порядък:

$$ \left|\begin(array)(cc) 5 & 2 \\ 7 & 3 \end(array) \right|=5\cdot 3-2\cdot 7=1. $$

Този минор не е равен на нула. Извод: сред минорите от втори ред има поне един различен от нула. Следователно $\rang A≥ 2$. Трябва да преминем към изучаване на непълнолетни от трети ред.

Ако изберем колона № 2 или колона № 4 за образуване на минори от трети ред, тогава тези минори ще бъдат равни на нула (тъй като ще съдържат нулева колона). Остава да се провери само един минор от трети ред, чиито елементи са разположени в пресечната точка на колони № 1, № 3, № 5 и редове № 1, № 2, № 3. Нека запишем този минор и да намерим стойността му:

$$ \left|\begin(array)(ccc) 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end(array) \right|=-20-18-14 +16+21+15=0. $$

И така, всички минори от трети ред са равни на нула. Последният ненулев минор, който компилирахме, беше от втори порядък. Заключение: максималният ред на второстепенните, сред които има поне един различен от нула, е 2. Следователно $\rang A=2$.

Отговор: $\rang A=2$.

Пример №2

Намерете ранга на матрицата $A=\left(\begin(array) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0 \\ 9 & 7 & 8 & -7 \end(array) \right)$.

Имаме квадратна матрица от четвърти ред. Нека веднага да отбележим, че рангът на тази матрица не надвишава 4, т.е. $\rang A≤ 4$. Нека започнем да намираме ранга на матрицата.

Сред второстепенните елементи от първи ред (т.е. сред елементите на матрицата $A$) има поне един, който не е равен на нула, следователно $\rang A≥ 1$. Нека да преминем към проверка на непълнолетни от втори ред. Например в пресечната точка на редове № 2, № 3 и колони № 1 и № 2 получаваме следния минор от втори ред: $\left| \begin(масив) (cc) 4 & -2 \\ -5 & 0 \end(масив) \right|$. Нека го изчислим:

$$\ляво| \begin(масив) (cc) 4 & -2 \\ -5 & 0 \end(масив) \right|=0-10=-10. $$

Сред минори от втори ред има поне един, който не е равен на нула, така че $\rang A≥ 2$.

Да преминем към минори от трети ред. Да намерим, например, минор, чиито елементи са разположени в пресечната точка на редове № 1, № 3, № 4 и колони № 1, № 2, № 4:

$$\ляво | \begin(масив) (cccc) -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end(масив) \right|=105-105=0. $$

Тъй като този минор от трети ред се оказа равен на нула, е необходимо да се изследва друг минор от трети ред. Или всички те ще бъдат равни на нула (тогава рангът ще бъде равен на 2), или сред тях ще има поне един, който не е равен на нула (тогава ще започнем да изучаваме минори от четвърти ред). Нека разгледаме минор от трети ред, чиито елементи са разположени в пресечната точка на редове № 2, № 3, № 4 и колони № 2, № 3, № 4:

$$\ляво| \begin(масив) (ccc) -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end(масив) \right|=-28. $$

Сред минори от трети ред има поне един различен от нула, така че $\rang A≥ 3$. Да преминем към проверката на непълнолетните от четвърти ред.

Всеки минор от четвърти ред се намира в пресечната точка на четири реда и четири колони на матрицата $A$. С други думи, минорът от четвърти ред е детерминантата на матрицата $A$, тъй като тази матрица съдържа 4 реда и 4 колони. Детерминантата на тази матрица е изчислена в пример № 2 от темата „Намаляване на реда на детерминантата в ред (колона)“, така че нека просто вземем готовия резултат:

$$\ляво| \begin(масив) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end (масив)\right|=86. $$

Така че минорът от четвърти ред не е равен на нула. Вече не можем да образуваме минори от пети ред. Заключение: най-високият ред на второстепенните, сред които има поне един различен от нула, е 4. Резултат: $\rang A=4$.

Отговор: $\rang A=4$.

Пример №3

Намерете ранга на матрицата $A=\left(\begin(array) (cccc) -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end( масив) \right)$.

Нека веднага да отбележим, че тази матрица съдържа 3 реда и 4 колони, така че $\rang A≤ 3$. В предишните примери започнахме процеса на намиране на ранга, като разгледахме второстепенни от най-малкия (първи) ред. Тук ще се опитаме незабавно да проверим непълнолетните от възможно най-висок порядък. За матрицата $A$ това са минори от трети ред. Нека разгледаме минор от трети ред, чиито елементи се намират в пресечната точка на редове № 1, № 2, № 3 и колони № 2, № 3, № 4:

$$\ляво| \begin(масив) (ccc) 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end(масив) \right|=-8-60-20=-88. $$

И така, най-високият ред на второстепенните, сред които има поне един, който не е равен на нула, е 3. Следователно рангът на матрицата е 3, т.е. $\rang A=3$.

Отговор: $\rang A=3$.

Като цяло, намирането на ранг на матрица по дефиниция е в общия случай доста трудоемка задача. Например, сравнително малка матрица с размер $5\times 4$ има 60 второстепенни лица. И дори ако 59 от тях са равни на нула, тогава 60-то второстепенно може да се окаже различно от нула. След това ще трябва да изучавате минори от трети ред, от които тази матрица има 40 броя. Обикновено те се опитват да използват по-малко тромави методи, като метода на граничещите второстепенни или метода на еквивалентните трансформации.

Нека е дадена някаква матрица:

.

Нека изберем в тази матрица произволни низове и произволни колони
. След това определителят ти ред, съставен от матрични елементи
, разположен в пресечната точка на избрани редове и колони, се нарича минор матрица от ти ред
.

Определение 1.13.Ранг на матрицата
е най-големият ред на ненулевия минор на тази матрица.

За да се изчисли ранга на матрица, трябва да се вземат предвид всички нейни минори от най-нисък ред и ако поне един от тях е различен от нула, да се премине към разглеждане на минори от най-висок ред. Този подход за определяне на ранга на матрица се нарича граничен метод (или метод на гранични второстепенни).

Задача 1.4.Използвайки метода на граничещи второстепенни, определете ранга на матрицата
.

.

Помислете за кантиране от първи ред, например,
. След това преминаваме към разглеждане на кантове от втори ред.

Например,
.

И накрая, нека анализираме границата от трети ред.

.

Така че най-високият ред на ненулев минор е 2, следователно
.

Когато решавате задача 1.4, можете да забележите, че редица граничещи минори от втори ред са различни от нула. В това отношение се прилага следната концепция.

Определение 1.14.Базисен минор на матрица е всеки ненулев минор, чийто ред е равен на ранга на матрицата.

Теорема 1.2.(Базисна малка теорема). Базисните редове (базисните колони) са линейно независими.

Забележете, че редовете (колоните) на матрицата са линейно зависими тогава и само ако поне един от тях може да бъде представен като линейна комбинация от останалите.

Теорема 1.3.Броят на линейно независимите редове на матрицата е равен на броя на линейно независимите колони на матрицата и е равен на ранга на матрицата.

Теорема 1.4.(Необходимо и достатъчно условие детерминантата да е равна на нула). За да определител -та поръчка е било равно на нула, е необходимо и достатъчно неговите редове (колони) да са линейно зависими.

Изчисляването на ранга на матрица въз основа на нейната дефиниция е твърде тромаво. Това става особено важно за матрици от висок ред. В тази връзка на практика рангът на матрицата се изчислява въз основа на прилагането на теореми 10.2 - 10.4, както и използването на понятията за еквивалентност на матрицата и елементарни трансформации.

Определение 1.15.Две матрици
И се наричат ​​еквивалентни, ако ранговете им са равни, т.е.
.

Ако матрици
И са еквивалентни, тогава обърнете внимание
 .

Теорема 1.5.Рангът на матрицата не се променя поради елементарни трансформации.

Ще наричаме елементарни матрични трансформации
някоя от следните операции върху матрица:

Замяна на редове с колони и колони със съответните редове;

Пренареждане на редове на матрица;

Зачертаване на линия, чиито елементи са нула;

Умножение на низ с число, различно от нула;

Добавяне към елементите на една линия на съответните елементи на друга линия, умножени по същото число
.

Следствие от теорема 1.5.Ако матрицата
получени от матрица използвайки краен брой елементарни трансформации, след това матрицата
И са еквивалентни.

Когато се изчислява рангът на матрица, тя трябва да се редуцира до трапецовидна форма, като се използва краен брой елементарни трансформации.

Определение 1.16.Ще наречем трапецовидна форма на матрично представяне, когато в граничния минор от най-висок порядък, различен от нула, всички елементи под диагоналните изчезват. Например:

.

Тук
, матрични елементи
отидете на нула. Тогава формата на представяне на такава матрица ще бъде трапецовидна.

По правило матриците се редуцират до трапецовидна форма с помощта на алгоритъма на Гаус. Идеята на алгоритъма на Гаус е, че чрез умножаване на елементите от първия ред на матрицата по съответните фактори се постига, че всички елементи от първата колона, разположени под елемента
, ще се превърне в нула. След това, умножавайки елементите на втората колона по съответните фактори, гарантираме, че всички елементи на втората колона, разположени под елемента
, ще се превърне в нула. След това продължете по същия начин.

Задача 1.5.Определете ранга на матрица, като я намалите до трапецовидна форма.

.

За да улесните използването на алгоритъма на Гаус, можете да размените първия и третия ред.








.

Очевидно е, че тук
. Въпреки това, за да приведете резултата в по-елегантна форма, можете допълнително да продължите да трансформирате колоните.










.

Теорема (за коректността на определяне на ранговете).Нека всички минори на матрицата A m × n (\displaystyle A_(m\умножено по n))поръчка k (\displaystyle k)са равни на нула ( M k = 0 (\displaystyle M_(k)=0)). Тогава ∀ M k + 1 = 0 (\displaystyle \forall M_(k+1)=0), ако съществуват. Модел:/рамка

Свързани определения

Имоти

• Теорема (за базисния минор):Позволявам r = ранг ⁡ A , M r (\displaystyle r=\име на оператор (ранг) A,M_(r))- базис минор на матрицата A (\displaystyle A), Тогава:
• Последствия:
• Теорема (за инвариантността на ранга при елементарни трансформации):Нека въведем обозначение за матрици, получени една от друга чрез елементарни трансформации. Тогава е вярно следното твърдение: Ако A ∼ B (\displaystyle A\sim B), тогава ранговете им са равни.
• Теорема на Кронекер-Капели:Система от линейни алгебрични уравнения е последователна тогава и само ако рангът на нейната основна матрица е равен на ранга на нейната разширена матрица. В частност:
  • Броят на основните променливи на системата е равен на ранга на системата.
  • Съгласувана система ще бъде дефинирана (решението й е уникално), ако рангът на системата е равен на броя на всички нейни променливи.
• Неравенството на Силвестър:Ако АИ Бразмерни матрици m x nИ n x k, Че

r a n k A B ≥ r a n k A + r a n k B − n (\displaystyle rankAB\geq rankA+rankB-n)

Това е частен случай на следното неравенство.

• Неравенството на Фробениус:Ако AB, BC, ABC са правилно определени, тогава

r a n k A B C ≥ r a n k A B + r a n k B C − r a n k B (\displaystyle rankABC\geq rankAB+rankBC-rankB)

Линейна трансформация и ранг на матрицата

Позволявам A (\displaystyle A)- размерна матрица m × n (\displaystyle m\times n)над полето C (\displaystyle C)(или R (\displaystyle R)). Позволявам T (\displaystyle T)- съответстваща линейна трансформация A (\displaystyle A)на стандартна база; означава, че T (x) = A x (\displaystyle T(x)=Ax). Ранг на матрицата A (\displaystyle A) е измерението на диапазона на трансформация T (\displaystyle T).

Методи

Има няколко метода за намиране на ранга на матрица:

• Метод на елементарна трансформация

Рангът на матрицата е равен на броя на ненулевите редове в матрицата след редуцирането й до ешалонна форма с помощта на елементарни трансформации на редовете на матрицата.

• Метод за ограждане на малолетни

Пуснете матрицата A (\displaystyle A)намерен ненулев минор k (\displaystyle k)-та поръчка M (\displaystyle M). Да разгледаме всички непълнолетни (k + 1) (\displaystyle (k+1))-ти ред, включително (кантиране) второстепенен M (\displaystyle M); ако всички те са равни на нула, тогава рангът на матрицата е равен на k (\displaystyle k). В противен случай сред граничещите минори има ненулев и цялата процедура се повтаря.