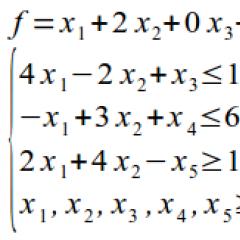Симплексният метод съдържа. Линейно програмиране

. Алгоритъм на симплексния метод

Пример 5.1.Решете следния проблем за линейно програмиране, като използвате симплексния метод:

решение:

аз повторение:

x3, x4, x5, x6 x1,x2. Ние изразяваме основните променливи по отношение на свободните:

Привеждаме целевата функция до следния вид:

Въз основа на получения проблем ще формираме началната симплексна таблица:

Таблица 5.3

Първоначална симплексна таблица

				Прогнозни отношения

Според дефиницията на основното решение, свободните променливи са равни на нула, а стойностите на основните променливи са равни на съответните стойности на свободните числа, т.е.:

Етап 3: проверка на съвместимостта на системата от ограничения на LLP.

При тази итерация (в Таблица 5.3) знакът за несъответствие на системата за ограничения (характеристика 1) не беше разкрит (т.е. няма ред с отрицателно свободно число (с изключение на линията на целевата функция), която не съдържа най-малко един отрицателен елемент (т.е. отрицателен коефициент за свободна променлива)).

При тази итерация (в таблица 5.3) знакът за неограниченост на целевата функция (знак 2) не беше разкрит (т.е. няма колона с отрицателен елемент в реда на целевата функция (с изключение на колоната със свободни числа) в който би имало поне един положителен елемент) .

Тъй като намереното основно решение не съдържа отрицателни компоненти, то е допустимо.

Етап 6: проверка на оптималността.

Намереното основно решение не е оптимално, тъй като според критерия за оптималност (знак 4) не трябва да има отрицателни елементи в реда на целевата функция (свободният номер на тази линия не се взема предвид при разглеждането на този знак ). Следователно, според алгоритъма на симплексния метод, преминаваме към 8-ми етап.

Тъй като намереното основно решение е допустимо, ще търсим разделящата колона по следната схема: определяме колоните с отрицателни елементи в реда на целевата функция (с изключение на колоната със свободни числа). Според таблица 5.3 има две такива колони: колоната " x1" и колона " x2". От такива колони се избира тази, която съдържа най-малкия елемент в реда на целевата функция. Тя ще се реши. говорител" x2' съдържа най-малкия елемент (-3) в сравнение с колоната ' x1

За да определим разрешителния низ, намираме положителните изчислени съотношения на свободните числа към елементите на разрешителната колона, низът, който съответства на най-малкото положително изчислено съотношение, се приема като разрешен.

Таблица 5.4

Първоначална симплексна таблица

В таблица 5.4 най-малкото положително съотношение на оценка съответства на реда " x5“, следователно, то ще бъде разрешаващо.

Елементът, разположен в пресечната точка на разрешаващата колона и разрешаващата линия, се приема като разрешаващ. В нашия пример това е елементът, който се намира в пресечната точка на линията " x5» и колони « x2».

Разделящият елемент показва една основна и една свободна променливи, които трябва да бъдат разменени в симплексната таблица, за да се премине към новото „подобрено“ основно решение. В този случай това са променливи. x5и x2, в новата симплексна таблица (таблица 5.5) ги разменяме.

9.1. Разрешаване на трансформация на елемент.

Разрешителният елемент от таблица 5.4 се трансформира, както следва:

Въвеждаме получения резултат в подобна клетка в таблица 5.5.

9.2. Разрешаване на преобразуване на низове.

Елементите на разрешителната линия на таблица 5.4 са разделени на разрешителния елемент на тази симплексна таблица, резултатите се вписват в подобни клетки на новата симплексна таблица (таблица 5.5). Трансформациите на елементите на разрешаващия низ са дадени в Таблица 5.5.

9.3. Разрешителна трансформация на колона.

Елементите на разделителната колона от таблица 5.4 се разделят на разделящия елемент на тази симплексна таблица и резултатът се взема с противоположен знак. Получените резултати се вписват в подобни клетки на новата симплексна таблица (таблици 5.5). Трансформациите на елементи от разделителната колона са дадени в Таблица 5.5.

9.4. Преобразуване на останалите елементи от симплексната таблица.

Преобразуването на други елементи от симплексната таблица (т.е. елементи, които не са разположени в разделящия ред и разделящата колона) се извършва съгласно правилото "правоъгълник".

Например, помислете за трансформацията на елемент, разположен в пресечната точка на низа " x3” и колони „”, условно го обозначават като „ x3". В таблица 5.4 мислено начертаваме правоъгълник, единият връх на който се намира в клетката, чиято стойност се трансформира (т.е. в клетката " x3”), а другият (диагонален връх) е в клетка с разделящ елемент. Другите два върха (на втория диагонал) са еднозначно определени. Тогава трансформираната стойност на клетката " x3"ще бъде равна на предишната стойност на тази клетка минус дроб, в знаменателя на която е разделящият елемент (от таблица 5.4), а в числителя продуктът на два други неизползвани върха, т.е.:

« x3»: .

Стойностите на други клетки се преобразуват по подобен начин:

« x3 x1»: ;

« x4»: ;

« x4 x1»: ;

« x6»: ;

« x6 x1»: ;

«»: ;

« x1»: .

В резултат на тези трансформации е получена нова симплексна таблица (таблица 5.5).

II повторение:

Етап 1: съставяне на симплексна таблица.

Таблица 5.5

Симплексна масаII итерации

				Изчислено отношения

Етап 2: определяне на основното решение.

В резултат на симплексните трансформации се получава ново основно решение (таблица 5.5):

Както можете да видите, с това основно решение стойността на целевата функция =15, което е повече, отколкото при предишното основно решение.

Не е установено несъответствие на системата от ограничения в съответствие със знак 1 в таблица 5.5.

Етап 4: проверка на ограничеността на целевата функция.

Неограничеността на целевата функция в съответствие със знак 2 в Таблица 5.5 не беше разкрита.

Етап 5: проверка на допустимостта на намереното основно решение.

Намереното основно решение в съответствие с характеристика 4 не е оптимално, тъй като редът на целевата функция на симплексната таблица (Таблица 5.5) съдържа отрицателен елемент: -2 (свободният номер на тази линия не се взема предвид при разглеждането на това отличителен белег). Така че нека преминем към стъпка 8.

Етап 8: дефиниране на активиращия елемент.

8.1. Определение на колона за разделителна способност.

Намереното основно решение е допустимо, определяме колоните с отрицателни елементи в реда на целевата функция (с изключение на колоната със свободни числа). Според таблица 5.5 има само една такава колона: " x1". Следователно ние го приемаме като разрешено.

8.2. Разрешителна дефиниция на низ.

Според получените стойности на положителните изчислени съотношения в таблица 5.6, минимумът е съотношението, съответстващо на реда " x3". Следователно ние го приемаме като разрешено.

Таблица 5.6

Симплексна масаII итерации

				Изчислено отношения
				3/1=3 – мин

Етап 9: трансформация на симплексната таблица.

Трансформациите на симплексната таблица (Таблица 5.6) се извършват по същия начин, както в предишната итерация. Резултатите от трансформациите на елементи от симплексната таблица са показани в Таблица 5.7.

III повторение

Въз основа на резултатите от симплексните трансформации от предишната итерация, ние съставяме нова симплексна таблица:

Таблица 5.7

Симплексна масаIII итерации

				Изчислено отношения

Етап 2: определяне на основното решение.

В резултат на симплексните трансформации се получава ново основно решение (таблица 5.7):

Етап 3: проверка на съвместимостта на системата от ограничения.

Не е установено несъответствие на системата от ограничения в съответствие със знак 1 в таблица 5.7.

Етап 4: проверка на ограничеността на целевата функция.

Неограничеността на целевата функция в съответствие със знак 2 в таблица 5.7 не беше разкрита.

Етап 5: проверка на допустимостта на намереното основно решение.

Намереното основно решение по критерий 3 е допустимо, тъй като не съдържа отрицателни компоненти.

Етап 6: проверка на оптималността на намереното основно решение.

Намереното основно решение в съответствие с характеристика 4 не е оптимално, тъй като редът на целевата функция на симплексната таблица (Таблица 5.7) съдържа отрицателен елемент: -3 (свободният номер на този ред не се взема предвид при разглеждането на това отличителен белег). Така че нека преминем към стъпка 8.

Етап 8: дефиниране на активиращия елемент.

8.1. Определение на колона за разделителна способност.

Намереното основно решение е допустимо, определяме колоните с отрицателни елементи в реда на целевата функция (с изключение на колоната със свободни числа). Според таблица 5.7 има само една такава колона: " x5". Следователно ние го приемаме като разрешено.

8.2. Разрешителна дефиниция на низ.

Според получените стойности на положителни оценени отношения в таблица 5.8, минимумът е отношението, съответстващо на реда " x4". Следователно ние го приемаме като разрешено.

Таблица 5.8

Симплексна масаIII итерации

				Изчислено отношения
				5/5=1 – мин

Етап 9: трансформация на симплексната таблица.

Трансформациите на симплексната таблица (Таблица 5.8) се извършват по същия начин, както в предишната итерация. Резултатите от трансформациите на елементите на симплексната таблица са показани в Таблица 5.9.

IV повторение

Етап 1: изграждане на нова симплексна маса.

Въз основа на резултатите от симплексните трансформации от предишната итерация, ние съставяме нова симплексна таблица:

Таблица 5.9

Симплексна масаIV итерации

				Изчислено отношения
			–(–3/5)=3/5
			–(1/5)=–1/5
			–(9/5)=–9/5
			–(–3/5)=3/5

Етап 2: определяне на основното решение.

В резултат на симплексните трансформации е получено ново основно решение, съгласно таблица 5.9, решението е както следва:

Етап 3: проверка на съвместимостта на системата от ограничения.

Не е разкрита несъответствие на системата от ограничения в съответствие с характеристика 1 в таблица 5.9.

Етап 4: проверка на ограничеността на целевата функция.

Неограничеността на целевата функция в съответствие със знак 2 в таблица 5.9 не беше разкрита.

Етап 5: проверка на допустимостта на намереното основно решение.

Намереното основно решение по критерий 3 е допустимо, тъй като не съдържа отрицателни компоненти.

Етап 6: проверка на оптималността на намереното основно решение.

Основното решение, намерено в съответствие с характеристика 4, е оптимално, тъй като няма отрицателни елементи в реда на целевата функция на симплексната таблица (Таблица 5.9) (свободният номер на този ред не се взема предвид при разглеждането на тази характеристика) .

Етап 7: проверка на алтернативното решение.

Намереното решение е единственото, тъй като в реда на целевата функция няма нулеви елементи (Таблица 5.9) (свободният номер на тази линия не се взема предвид при разглеждането на тази характеристика).

Отговор: оптималната стойност на целевата функция на разглежданата задача =24, която се постига при.

Пример 5.2.Решете горния проблем за линейно програмиране, като приемете, че целевата функция е минимизирана:

решение:

аз повторение:

Етап 1: формиране на първоначалната симплексна таблица.

Оригиналната задача за линейно програмиране е дадена в стандартна форма. Нека го приведем до канонична форма, като във всяко от ограниченията на неравенството въведем допълнителна неотрицателна променлива, т.е.

В получената система от уравнения приемаме като разрешени (основни) променливи x3, x4, x5, x6, то свободните променливи са x1,x2. Изразяваме основните променливи чрез свободните.

Обмисли симплекс методза решаване на задачи на линейно програмиране (LP). Основава се на прехода от един референтен план към друг, при който стойността на целевата функция се увеличава.

Алгоритъмът на симплексния метод е както следва:

1. Превеждаме оригиналния проблем в канонична форма, като въвеждаме допълнителни променливи. За неравенство от вида ≤ се въвеждат допълнителни променливи със знак (+), но ако от вида ≥, тогава със знак (-). В целевата функция се въвеждат допълнителни променливи със съответните знаци с коефициент равен на 0 , защото целевата функция не трябва да променя своето икономическо значение.
2. Издават се вектори Пиот коефициентите на променливите и колоната със свободни членове. Това действие определя броя на единичните вектори. Правилото е, че трябва да има толкова единични вектори, колкото има неравенства в системата на ограниченията.
3. След това първоначалните данни се въвеждат в симплексната таблица. Единичните вектори се въвеждат в базата и като се изключат от основата се намира оптималното решение. Коефициентите на целевата функция се записват с противоположен знак.
4. Критерият за оптималност за LP проблема е, че решението е оптимално, ако е в е– ред всички коефициенти са положителни. Правило за намиране на колона за разрешения – Прегледано ее низ и сред отрицателните му елементи се избира най-малкият. вектор Пинеговото съдържание става разрешително. Правилото за избор на разделящ елемент - компилират се съотношенията на положителните елементи на разделителната колона към елементите на вектора P 0и числото, което дава най-малкото съотношение, става разделящ елемент, спрямо който ще бъде преизчислена симплексната таблица. Низът, съдържащ този елемент, се нарича низ за разрешаване. Ако няма положителни елементи в колоната за резолюция, тогава проблемът няма решение. След определяне на разделящия елемент, те пристъпват към преизчисляване на нова симплексна таблица.
5. Правила за попълване на нова симплексна таблица. На мястото на разделящия елемент се поставя един, а другите елементи се приемат за равни 0 . Разделящият вектор се добавя към основата, от която съответният нулев вектор се изключва, а останалите базисни вектори се записват непроменени. Елементите на разрешителната линия се разделят на разрешителния елемент, а останалите елементи се преизчисляват според правилото на правоъгълниците.
6. Това се прави до е– всички елементи на низа няма да станат положителни.

Помислете за решението на проблема, като използвате горния алгоритъм.
дадено:

Привеждаме проблема в каноничната форма:

Ние съставяме вектори:

Попълнете симплексната таблица:

:
Преизчисляване на първия елемент на вектора P 0, за което правим правоъгълник от числа: и получаваме: .

Извършваме подобни изчисления за всички останали елементи на симплексната таблица:

В получения план е– низът съдържа един отрицателен елемент – (-5/3), вектори P1. Той съдържа в колоната си единствения положителен елемент, който ще бъде разделящият елемент. Нека преизчислим таблицата по отношение на този елемент:

Липсата на отрицателни елементи в е- низ означава намерен оптимален план:
F* = 36/5, X = (12/5, 14/5, 8, 0, 0).

• Ашманов С. А. Линейно програмиране, М: Наука, 1998,
• Wentzel E.S. Оперативни изследвания, М: Съветско радио, 2001 г.,
• Кузнецов Ю.Н., Кузубов В.И., Волошенко А.Б. Математическо програмиране, М: Висше училище, 1986

Персонализирано решение за линейно програмиране

Можете да поръчате всякакви задачи в тази дисциплина на нашия уебсайт. Можете да прикачите файлове и да посочите крайни срокове на

Този метод е метод за целенасочено изброяване на референтни решения на задача за линейно програмиране. Той позволява краен брой стъпки или за намиране на оптималното решение, или за установяване, че няма оптимално решение.

Основното съдържание на симплексния метод е както следва:

1. Посочете метод за намиране на оптималното референтно решение
2. Посочете метода за преход от едно еталонно решение към друго, при което стойността на целевата функция ще бъде по-близка до оптималната, т.е. посочете начин за подобряване на референтното решение
3. Задайте критериите, които ви позволяват своевременно да спрете изброяването на референтни решения на оптималното решение или да следвате заключението, че няма оптимално решение.

Алгоритъм на симплексния метод за решаване на задачи за линейно програмиране

За да решите проблема по симплексния метод, трябва да направите следното:

1. Приведете проблема в канонична форма
2. Намерете първоначално референтно решение с "единична основа" (ако няма референтно решение, тогава проблемът няма решение поради несъвместимостта на системата от ограничения)
3. Изчислете оценките на векторните разширения по отношение на основата на референтното решение и попълнете таблицата на симплексния метод
4. Ако критерият за уникалност на оптималното решение е изпълнен, тогава решението на проблема приключва
5. Ако условието за съществуване на набор от оптимални решения е изпълнено, тогава чрез просто изброяване се намират всички оптимални решения

Пример за решаване на задачата по симплексния метод

Пример 26.1

Решете проблема с помощта на симплексния метод:

решение:

Привеждаме проблема в канонична форма.

За да направим това, въвеждаме допълнителна променлива x 6 с коефициент +1 в лявата част на първото ограничение на неравенството. Променливата x 6 е включена в целевата функция с коефициент нула (т.е. не е включена).

Получаваме:

Намираме първоначалното референтно решение. За да направим това, ние приравняваме свободните (неразрешени) променливи на нула x1 = x2 = x3 = 0.

Получаваме референтно решение X1 = (0.0.0.24.30.6) с база единица B1 = (A4, A5, A6).

Изчисли оценки за векторно разлаганеусловия на базата на еталонния разтвор по формулата:

Δ k \u003d C b X k - c k

• C b = (с 1 , с 2 , ... , с m) е векторът на коефициентите на целевата функция с основни променливи
• X k = (x 1k , x 2k , ... , x mk) е векторът на разширение на съответния вектор A k по отношение на основата на референтното решение
• C k - коефициент на целевата функция за променливата x k.

Оценките на векторите, включени в базата, винаги са равни на нула. Референтното решение, коефициентите на разширения и оценките на разширенията на векторите на условия по отношение на основата на еталонното решение са записани в симплексна маса:

Над таблицата, за удобство при изчисляване на оценките, са записани коефициентите на целевата функция. Първата колона "B" съдържа векторите, включени в основата на референтното решение. Редът на записване на тези вектори съответства на броя на разрешените неизвестни в уравненията на ограниченията. Във втората колона на таблицата "С b" се записват коефициентите на целевата функция с основни променливи в същия ред. При правилно подреждане на коефициентите на целевата функция в колоната "C b", оценките на единичните вектори, включени в базата, винаги са равни на нула.

В последния ред на таблицата с оценки на Δ k в колоната "A 0" стойностите на целевата функция са записани върху референтното решение Z(X 1).

Първоначалното референтно решение не е оптимално, тъй като в задачата за максимум оценките Δ 1 = -2, Δ 3 = -9 за векторите A 1 и A 3 са отрицателни.

Съгласно теоремата за подобряване на референтното решение, ако в максималната задача поне един вектор има отрицателна оценка, тогава може да се намери ново референтно решение, при което стойността на целевата функция ще бъде по-голяма.

Нека определим кой от двата вектора ще доведе до по-голямо увеличение на целевата функция.

Увеличението на целевата функция се намира по формулата: .

Изчисляваме стойностите на параметъра θ 01 за първата и третата колона по формулата:

Получаваме θ 01 = 6 за l = 1, θ 03 = 3 за l = 1 (таблица 26.1).

Откриваме увеличението на целевата функция, когато първият вектор ΔZ 1 = - 6 * (- 2) = 12 се въведе в основата, а третият вектор ΔZ 3 = - 3 * (- 9) = 27.

Следователно, за по-бърз подход към оптималното решение, е необходимо да се въведе вектора A3 в основата на еталонното решение вместо първия вектор на базата A6, тъй като минимумът на параметъра θ 03 се достига в първия ред (l = 1).

Извършваме преобразуването на Йордан с елемента X13 = 2, получаваме второто референтно решение X2 = (0.0.3.21.42.0) с основа B2 = (A3, A4, A5). (таблица 26.2)

Това решение не е оптимално, тъй като векторът A2 има отрицателна оценка Δ2 = - 6. За подобряване на решението е необходимо да се въведе вектор A2 в основата на референтното решение.

Определяме номера на вектора, получен от основата. За да направим това, изчисляваме параметъра θ 02 за втората колона, той е равен на 7 за l = 2. Следователно, извличаме втория базисен вектор A4 от основата. Извършваме трансформацията на Йордан с елемента x 22 = 3, получаваме третото референтно решение X3 = (0.7.10.0.63.0) B2 = (A3, A2, A5) (таблица 26.3).

Това решение е единственото оптимално, тъй като за всички вектори, които не са включени в базата, оценките са положителни

Δ 1 = 7/2, Δ 4 = 2, Δ 6 = 7/2.

Отговор: max Z(X) = 201 при X = (0,7,10,0,63).

Метод на линейно програмиране в икономическия анализ

Метод на линейно програмиранедава възможност да се обоснове най-оптималното икономическо решение при строги ограничения, свързани с използваните в производството ресурси (основни активи, материали, трудови ресурси). Прилагането на този метод в икономическия анализ ни позволява да решаваме проблеми, свързани основно с планирането на дейността на организацията. Този метод помага да се определят оптималните стойности на продукцията, както и насоките за най-ефективно използване на производствените ресурси, с които разполага организацията.

С помощта на този метод се извършва решаването на така наречените екстремни задачи, което се състои в намиране на екстремни стойности, тоест на максимума и минимума на функциите на променливите.

Този период се основава на решаване на система от линейни уравнения в случаите, когато анализираните икономически явления са свързани с линейна, строго функционална зависимост. Методът на линейно програмиране се използва за анализ на променливи при наличие на определени ограничаващи фактори.

Доста често срещано е решението на така наречения транспортен проблем с метода на линейно програмиране. Съдържанието на тази задача е да се сведат до минимум разходите, направени във връзка с експлоатацията на превозни средства при съществуващите ограничения по отношение на броя на превозните средства, тяхната товароподемност, продължителността на тяхната работа, ако има нужда от обслужване на максимален брой клиенти .

В допълнение, този метод се използва широко при решаването на проблема с планирането. Тази задача се състои в такова разпределение на времето на функциониране на персонала на тази организация, което би било най-приемливо както за членовете на този персонал, така и за клиентите на организацията.

Целта е да се увеличи максимално броят на обслужваните клиенти, като се ограничи броят на наличните служители и работното време.

По този начин методът на линейно програмиране е много разпространен при анализа на разположението и използването на различни видове ресурси, както и в процеса на планиране и прогнозиране на дейността на организациите.

Въпреки това, математическото програмиране може да се приложи и към онези икономически явления, връзката между които не е линейна. За целта могат да се използват методи на нелинейно, динамично и изпъкнало програмиране.

Нелинейното програмиране разчита на нелинейния характер на целевата функция или ограниченията, или и двете. Формите на целевата функция и неравенствата на ограниченията при тези условия могат да бъдат различни.

Нелинейното програмиране се използва в икономическия анализ, по-специално при установяване на връзката между показателите, изразяващи ефективността на дейността на организацията и обема на тази дейност, структурата на производствените разходи, пазарните условия и др.

Динамичното програмиране се основава на изграждане на дърво на решенията. Всяко ниво от това дърво служи като етап за определяне на последствията от предишното решение и за елиминиране на неефективни варианти на това решение. По този начин динамичното програмиране има многоетапен, многоетапен характер. Този тип програмиране се използва в икономическия анализ, за ​​да се намерят най-добрите варианти за развитие на организацията както сега, така и в бъдеще.

Изпъкналото програмиране е вид нелинейно програмиране. Този тип програмиране изразява нелинейния характер на връзката между резултатите от дейността на организацията и направените от нея разходи. Изпъкналото (иначе вдлъбнато) програмиране анализира изпъкнали целеви функции и изпъкнали ограничителни системи (характерни точки). Изпъкналото програмиране се използва при анализа на икономическата дейност с цел минимизиране на разходите, а вдлъбнатото програмиране се използва за максимизиране на доходите в условията на съществуващи ограничения върху действието на фактори, които влияят на анализираните показатели по обратен начин. Следователно, при разглежданите типове програмиране, изпъкналите целеви функции са минимизирани, а вдлъбнатите се максимизират.

Симплексен метод - това е метод на последователен преход от едно основно решение (върхът на полиедъра на решението) на системата от ограничения на задача за линейно програмиране към друго основно решение, докато целевата функция приеме оптималната стойност (максимум или минимум).

Симплексният метод е универсален метод, който може да реши всеки проблем с линейното програмиране, докато графичният метод е подходящ само за система с две променливи ограничения.

Симплексният метод е предложен от американския математик Р. Данциг през 1947 г., оттогава за нуждите на индустрията този метод често решава проблеми на линейно програмиране с хиляди променливи и ограничения.

Преди да преминем към алгоритъма на симплексния метод, няколко дефиниции.

Всяко неотрицателно решение на система от ограничения се нарича приемливо решение .

Нека има система мограничения от нпроменливи ( мн).

Допустимо основно решение е разтвор, съдържащ мнеотрицателен майор (основен ) променливи и н - м неосновни . (неосновни, или Безплатно ) променливи. Неосновните променливи в основното решение са равни на нула, докато основните променливи, като правило, са различни от нула, тоест са положителни числа.

Всякакви мсистемни променливи млинейни уравнения с нпроменливите се извикват главен , ако детерминантата на коефициентите при тях е различна от нула. След това останалото н - мпроменливите се извикват неосновни (или Безплатно ).

Алгоритъм на симплексния метод

• Етап 1. Приведете проблема с линейното програмиране в канонична форма. За да направите това, преместете свободните членове в дясната страна (ако сред тези свободни членове са отрицателни, след това умножете съответното уравнение или неравенство по - 1) и въведете допълнителни променливи във всяко ограничение (със знак плюс, ако е в първоначалното неравенство знакът е по-малък или равен на ", и със знак минус, ако "по-голям или равен на").
• Стъпка 2. Ако в получената система муравнения, тогава мвземете променливите като основни, изразете главните променливи чрез неосновните и намерете съответното основно решение. Ако намереното основно решение се окаже допустимо, преминете към допустимото основно решение.
• Стъпка 3. Изразете функцията на целта чрез второстепенните променливи на възможното основно решение. Ако се намери максимумът (минимумът) на линейната форма и в нейното изразяване няма неосновни променливи с отрицателни (положителни) коефициенти, тогава критерият за оптималност е изпълнен и полученото основно решение е оптимално - решението е приключило. Ако при намиране на максимума (минимума) на линейна форма нейният израз съдържа една или повече неосновни променливи с отрицателни (положителни) коефициенти, преминете към ново основно решение.
• Стъпка 4. От неосновните променливи, включени в линейната форма с отрицателни (положителни) коефициенти, изберете тази, която съответства на най-големия (модулен) коефициент, и го прехвърлете към основните. Преминете към стъпка 2.

Важни условия

Някои специални случаи са разгледани в отделни статии: кога максимална целева функция - безкрайност, кога системата няма решение, и когато оптималното решение не е единственото .

След това ще анализираме типичен пример, когато системата от ограничения е последователна и има краен оптимум и само един. Разновидност на симплексния метод е метод на разпространение за решаване на транспортния проблем .

Симплексен метод със симплексни таблици

Чрез конструирането на симплексни таблици е много по-лесно да се реши проблем за линейно програмиране, отколкото чрез алгебрични трансформации, което е показано в следващия параграф. Симплексните таблици са много визуални. Има няколко вида правила за работа със симплексни таблици. Ще анализираме правилото, което най-често се нарича правило за водеща колона и правило на водещия ред.

Би било полезно да отворите ръчните Действия с дроби в нов прозорец: има достатъчно от тях, дроби в задачи по симплексния метод, меко казано.

Пример.

Ние въвеждаме допълнителни неотрицателни променливи и свеждаме тази система от неравенства до еквивалентна система от уравнения

.

Това беше направено в съответствие със следното правило: ако знакът в първоначалното ограничение е "по-малък или равен на", тогава трябва да се добави допълнителната променлива, а ако "по-голям или равен на", тогава допълнителната променлива трябва да бъде изваден.

Въведените допълнителни променливи се приемат като основни (основни). Тогава и са неосновни (безплатни) променливи.

Изразявайки основните (основни) променливи по отношение на неосновните (свободни), получаваме

Ние също така изразяваме целевата функция по отношение на неосновни (безплатни) променливи:

От коефициентите на променливите (неизвестни) изграждаме първата симплексна таблица.

маса 1
Основни неизвестни	Безплатни членове	Свободни неизвестни		Помощни коефициенти
		X1	X2
X3	-2	1	-2
X4	-4	-1	-1
X5	2	1	-1
X6	6	0	1
Ф	0	-1	-2

Последният ред на таблицата, който съдържа целевата функция и коефициентите за свободните променливи в нея, ще се нарича индексен ред.

Полученото решение не е оптимално, тъй като коефициентите на свободните променливи в индексния ред са отрицателни. Тоест оптималното решение ще бъде това, при което коефициентите на свободните променливи в индексния ред ще бъдат по-големи или равни на нула.

За да преминете към следващата таблица, намерете най-голямото (модуло) от числата и . Това число е 2. Следователно водещата колона е колоната, в която е изписано

За да определим водещия ред, намираме минимума от съотношенията на свободните членове към елементите на водещата колона и ако числителят има положително число, а знаменателят е отрицателен, съотношението се счита за равно на безкрайност.

.

Следователно водещият ред е този, в който е написан

Следователно водещият елемент е -2.

Съставяме втората симплексна таблица.

Въвеждаме новия основен елемент в първия ред и въвеждаме колоната, в която е стоял, въвеждаме нова безплатна променлива

Попълнете първия ред. За да направите това, разделяме всички числа в началния ред на таблица 1 на водещия елемент и го записваме в съответната колона на първия ред на таблица 2, с изключение на числото в водещата колона, където реципрочната стойност на водещата елемент се записва (тоест един, разделен на водещия елемент).

Попълнете колоната със спомагателни коефициенти. За този номер на водещата колона на таблица 1, в допълнение към водещия елемент, пишем с противоположни знаци в колоната на помощните коефициенти на таблица 2.

таблица 2
Основни неизвестни	Безплатни членове	Свободни неизвестни		Помощни коефициенти
		X1	X3
X2	1	-1/2	-1/2
X4	-3	-3/2	-1/2	1
X5	3	1/2	-1/2	1
X6	5	1/2	1/2	-1
Ф	2	-2	-1	2

Който все още не е отворил в нов прозорец ръчните Действия с дроби, може да го направи сега, защото е време.

За да се получат останалите редове на таблица 2, числата, които вече са в първия ред на тази таблица, се умножават по спомагателния коефициент в реда, който се попълва, и към резултата добавяме числото от таблица 1, което е в същия ред с съответната променлива.

Например, за да получим свободния член от втория ред, умножаваме числото 1 по 1 и добавяме числото -4 от таблица 1. Получаваме -3. Намираме коефициента за във втория ред по същия начин: . Тъй като в предишната таблица няма колона с нова свободна променлива, коефициентът на втория ред в колоната на новата свободна променлива ще бъде (тоест от таблица 1 добавяме 0, тъй като в таблица 1 няма колона c).

Индексният ред се попълва по същия начин:

Така полученото решение отново не е оптимално, тъй като коефициентите на свободните променливи в индексния ред отново са отрицателни.

За да преминем към следващата симплексна таблица, намираме най-голямото (по абсолютна стойност) от числата и , тоест модулите на коефициентите в индексната линия. Това число е 2. Следователно водещата колона е колоната, която съдържа .

За да търсим водещия ред, нека намерим минималното съотношение на свободните членове към елементите на водещия ред. Получаваме:

.

Следователно водещият ред е този, в който е изписан, а водещият елемент е -3/2.

Съставяне на третата симплексна таблица

Записваме новата основна променлива на първия ред. В колоната, в която беше, въвеждаме нова безплатна променлива.

Първа линия:

Спомагателни коефициенти:

Таблица 3
Основни неизвестни	Безплатни членове	Свободни неизвестни		Помощни коефициенти
		X4	X3
X1	2	-2/3	1/3
X2	2	-1/3	-1/3	1/2
X5	2	1/3	-2/3	-1/2
X6	4	1/3	1/3	-1/2
Ф	6	-4/3	-1/3	2

Полученото решение отново не е оптимално, тъй като коефициентите на свободните неизвестни в индексния ред отново са отрицателни.

За да отидем до четвъртата симплексна таблица, нека намерим най-голямото от числата и . Това е число.

Следователно водещата колона е тази с .

Минимален модул на отношенията на свободните членове към елементите на водещата колона:

.

Следователно водещият ред е този, в който е изписан, а водещият елемент е 1/3.

В четвъртата симплексна таблица пишем новата основна променлива в първия ред. В колоната, където беше, пишем нова безплатна променлива.

Първа линия:

Спомагателни коефициенти:

Таблица 4
Основни неизвестни	Безплатни членове	Свободни неизвестни		Помощни коефициенти
		X5	X3
X4	6	3	-2
X1	6	2	-1	2/3
X2	4	1	-1	1/3
X6	2	-1	1	-1/3
Ф	14	4	-3	4/3

Изчисляване на останалите редове с помощта на примера на втория ред:

Полученото решение също не е оптимално, но вече е по-добро от предишните, тъй като един от коефициентите за свободните променливи в индексния ред е неотрицателен.

За да подобрим плана, нека преминем към следващата симплексна таблица.

Намерете най-голямото от числата 4 и . Това число е 4. Следователно водещата колона е .

За да намерите водещия ред, намерете

.

Следователно водещият ред е този, който съдържа . Но те вече бяха заедно сред свободните променливи. Следователно, за да прехвърлим следващата променлива от безплатна към основна, избираме друга водеща колона - тази, в която е написана.

За да намерите водещия ред, намерете

.

Следователно ключовият ред е този, в който е написан, а водещият елемент е 1.

В петата симплексна таблица новата основна променлива е записана на първия ред. В колоната, където беше, пишем нова безплатна променлива.

Първа линия:

Спомагателни коефициенти:

Таблица 5
Основни неизвестни	Безплатни членове	Свободни неизвестни		Помощни коефициенти
		X5	X6
X3	2	-1	1
X4	10			2
X1	8			1
X2	6			1
Ф	20	1	3	3

Нека се опитаме да разберем веднага дали решението не е оптимално. Следователно за останалите редове изчисляваме само свободните термини (за да разберем стойностите на основните променливи, когато свободните променливи са равни на нула) и коефициентите за свободните променливи в реда на индекса.

Безплатни членове:

Във втория ред;

В третия ред;

На четвъртия ред.

Индексен ред:

Разглеждаме симплексната таблица 5. Виждаме, че е получено оптималното решение, тъй като коефициентите за свободни неизвестни в индексния ред са неотрицателни.

Симплексен метод с алгебрични трансформации

Нека решим чрез алгебрични трансформации същия пример като в предишния параграф. Трябва да се отбележи, че при решаването на този тип симплексен метод е по-добре да не пишете целевата функция във формата , тъй като е лесно да се объркате в знаците. Но в този случай точката на алгоритъма, която определя критерия за оптималност, ще бъде модифицирана, както следва.

Ако се намери максимумът (минимумът) на линейната форма и в нейното изразяване няма неосновни променливи с положителни (отрицателни) коефициенти, тогава критерият за оптималност е изпълнен и полученото основно решение е оптимално - решението е приключило. Ако при намиране на максимума (минимума) на линейна форма нейният израз съдържа една или повече неосновни променливи с положителни (отрицателни) коефициенти, преминете към ново основно решение.

Пример.Намерете максимума на функция при ограничения

Стъпка I. Въвеждаме допълнителни неотрицателни променливи и свеждаме тази система от неравенства до еквивалентна система от уравнения

.

Въведените допълнителни променливи се приемат като основни, тъй като в този случай лесно се намира основното решение на системата. Тогава и са второстепенни променливи.

Изразявайки основните променливи в термините на неосновните, получаваме

Следователно, това разделение на променливите на основни и неосновни съответства на основното решение , което е невалидно (две променливи са отрицателни) и следователно не е оптимално. Нека преминем от това основно решение към подобрено.

За да решите коя променлива трябва да бъде преобразувана от неглавна в основна, разгледайте едно от двете налични уравнения на последната система с отрицателни свободни членове, например второто. Това показва, че и може да се преведе в основните променливи, тъй като в това уравнение те имат положителни коефициенти (следователно, когато се увеличат, а това ще се случи, ако преведем някоя от тях в основните променливи, променливата ще се увеличи).

Нека се опитаме да преведем в основната променлива. За да установим коя променлива трябва да се прехвърли от основната към неосновната, намираме абсолютната стойност на най-малкото съотношение на свободните членове на системата към коефициентите при . Ние имаме . Получава се от третото уравнение, което показва, че променливата трябва да се преобразува в неосновни, което е положително в първоначалното основно решение. Следователно, полученото основно решение, подобно на оригиналното, съдържа два отрицателни компонента, т.е. няма да има подобрение при прехода към такова основно решение.

Кратка теория

Решението на проблема

Изграждане на модели

Да обозначим съответно оборота на 1-ви, 2-ри и трети вид стоки.

Тогава целевата функция, изразяваща получената печалба:

Ограничения за материални и парични ресурси:

Освен това според смисъла на задачата

Получаваме следния проблем за линейно програмиране:

Попълваме симплексната таблица на 0-та итерация.

BP

Симплекс отношения

8

6

4

0

0

0

0

520

16

18

9

1

0

0

65/2

0

140

7

7

2

0

1

0

20

0

810

9

2

1

0

0

1

90

0

-8

-6

-4

0

0

0

Тъй като решаваме задачата за максимума, наличието на отрицателни числа в индексната линия при решаване на задачата за максимум показва, че не сме получили оптималното решение и че е необходимо да преминем от таблицата на 0-та итерация към следващият.

Преходът към следващата итерация се извършва, както следва:

Водещата колона съвпада.

Ключовият ред се определя от минималните съотношения на свободните членове и членовете на водещата колона (симплексни съотношения):

В пресечната точка на ключовата колона и ключовия ред намираме активиращия елемент, т.е. 7.

Сега започваме компилирането на 1-ва итерация. Вместо единичен вектор, ние въвеждаме вектор.

В новата таблица пишем 1 на мястото на разрешаващия елемент, всички останали елементи на ключовата колона са нули. Елементите на ключовия низ са разделени от разрешителния елемент. Всички останали елементи на таблицата се изчисляват по правилото за правоъгълник.

Получаваме таблицата от 1-ва итерация:

BP

Симплекс отношения

8

6

4

0

0

0

0

200

0

2

31/7

1

-16/7

0

1400/31

8

20

1

1

2/7

0

1/7

0

70

0

630

0

-7

-11/7

0

-9/7

1

-

160

0

2

-12/7

0

8/7

0

Ключовата колона за 1-ва итерация съответства на .

Намираме ключовата линия, за това дефинираме:

В пресечната точка на ключовата колона и ключовия ред намираме активиращия елемент, т.е. 31/7.

Извеждаме вектора от основата и въвеждаме вектора.

Получаваме таблицата от 2-ра итерация:

BP

Симплекс отношения

8

6

4

0

0

0

4

1400/31

0

14/31

1

7/31

-16/31

0

8

220/31

1

27/31

0

-2/31

9/31

0

0

21730/31

0

-195/31

0

11/31

-65/31

1

7360/31

0

86/31

0

12/31

8/31

0

В индексния ред всички членове са неотрицателни, така че се получава следното решение на проблема с линейното програмиране (изписваме го от колоната със свободни членове):

По този начин е необходимо да се продадат 7,1 хиляди рубли. стоки от 1-ви тип и 45,2 хиляди рубли. стоки от 3-ти вид. Стоки от 2-ри тип са нерентабилни за продажба. В този случай печалбата ще бъде максимална и ще възлиза на 237,4 хиляди рубли. При изпълнение на оптималния план оставащият ресурс от 3-ти тип ще бъде 701 единици.

Ако не се нуждаете от помощ сега, но може да се нуждаете от нея в бъдеще, тогава, за да не загубите контакт,