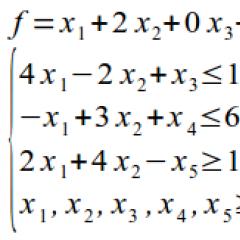Изпълнение и обучение на симплексен метод. Решаване на задачи за линейно програмиране по симплексния метод
Обмисли симплекс методза решаване на задачи на линейно програмиране (LP). Основава се на прехода от един референтен план към друг, при който стойността на целевата функция се увеличава.
Алгоритъмът на симплексния метод е както следва:
- Превеждаме оригиналния проблем в канонична форма, като въвеждаме допълнителни променливи. За неравенство от вида ≤ се въвеждат допълнителни променливи със знак (+), но ако от вида ≥, тогава със знак (-). В целевата функция се въвеждат допълнителни променливи със съответните знаци с коефициент равен на 0 , защото целевата функция не трябва да променя своето икономическо значение.
- Издават се вектори Пиот коефициентите на променливите и колоната със свободни членове. Това действие определя броя на единичните вектори. Правилото е, че трябва да има толкова единични вектори, колкото има неравенства в системата на ограниченията.
- След това първоначалните данни се въвеждат в симплексната таблица. Единичните вектори се въвеждат в базата и като се изключат от основата се намира оптималното решение. Коефициентите на целевата функция се записват с противоположен знак.
- Критерият за оптималност за LP проблема е, че решението е оптимално, ако е в е– ред всички коефициенти са положителни. Правило за намиране на колона за разрешения – Прегледано ее низ и сред отрицателните му елементи се избира най-малкият. вектор Пинеговото съдържание става разрешително. Правилото за избор на разделящ елемент - компилират се съотношенията на положителните елементи на разделителната колона към елементите на вектора P 0и числото, което дава най-малкото съотношение, става разделящ елемент, спрямо който ще бъде преизчислена симплексната таблица. Низът, съдържащ този елемент, се нарича низ за разрешаване. Ако няма положителни елементи в колоната за резолюция, тогава проблемът няма решение. След определяне на разделящия елемент, те пристъпват към преизчисляване на нова симплексна таблица.
- Правила за попълване на нова симплексна таблица. На мястото на разделящия елемент се поставя един, а другите елементи се приемат за равни 0 . Разделящият вектор се добавя към основата, от която съответният нулев вектор се изключва, а останалите базисни вектори се записват непроменени. Елементите на разрешителната линия се разделят на разрешителния елемент, а останалите елементи се преизчисляват според правилото на правоъгълниците.
- Това се прави до е– всички елементи на низа няма да станат положителни.
Помислете за решението на проблема, като използвате горния алгоритъм.
дадено:
Привеждаме проблема в каноничната форма:

Ние съставяме вектори:

Попълнете симплексната таблица:

:
Преизчисляване на първия елемент на вектора P 0, за което правим правоъгълник от числа: и получаваме:  .
.
Извършваме подобни изчисления за всички останали елементи на симплексната таблица:

В получения план е– низът съдържа един отрицателен елемент – (-5/3), вектори P1. Той съдържа в колоната си единствения положителен елемент, който ще бъде разделящият елемент. Нека преизчислим таблицата по отношение на този елемент:

Липсата на отрицателни елементи в е- низ означава намерен оптимален план:
F* = 36/5, X = (12/5, 14/5, 8, 0, 0).
- Ашманов С. А. Линейно програмиране, М: Наука, 1998,
- Wentzel E.S. Оперативни изследвания, М: Съветско радио, 2001 г.,
- Кузнецов Ю.Н., Кузубов В.И., Волошенко А.Б. Математическо програмиране, М: Висше училище, 1986
Персонализирано решение за линейно програмиране
Можете да поръчате всякакви задачи в тази дисциплина на нашия уебсайт. Можете да прикачите файлове и да посочите крайни срокове на
Симплексен метод- това е итеративен процес на насочено решаване на система от уравнения на стъпки, който започва с еталонно решение и в търсене на най-добрия вариант се движи по ъгловите точки на възможната област на решение, подобрявайки стойността на целевата функция докато целевата функция достигне оптималната стойност.Възлагане на услугата. Услугата е предназначена за онлайн решаване на проблеми с линейно програмиране (LPP) с помощта на симплексния метод в следните нотационни форми:
- под формата на симплексна таблица (метод на Йорданови трансформации); основна форма на запис;
- модифициран симплексен метод; под формата на колона; в линейна форма.
Инструкция. Изберете броя на променливите и броя на редовете (брой ограничения). Полученото решение се записва във файл на Word и Excel. В същото време не вземайте предвид ограниченията от типа x i ≥0. Ако няма ограничения в задачата за някои x i, тогава LLP трябва да бъде намален до KZLP или да използвате тази услуга. Решението автоматично определя употребата М-метод(симплексен метод с изкуствена основа) и двуетапен симплекс метод.
Следното също се използва с този калкулатор:
Графичен метод за решаване на LLP
Решение на транспортния проблем
Матрично решение за игра
Използвайки услугата онлайн, можете да определите цената на матрична игра (долни и горни граници), да проверите за седловина, да намерите решение на смесена стратегия, като използвате следните методи: минимакс, симплексен метод, графичен (геометричен) метод, Методът на Браун.
Екстремум на функция от две променливи
Проблеми с динамичното програмиране
Разпределете 5 хомогенни партиди стоки между три пазара по такъв начин, че да получите максимален доход от продажбата им. Приходът от продажбата на всеки пазар G(X) зависи от броя на продадените партиди стоки X и е представен в таблицата.
| Обем на продукта X (в партиди) | Доход G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
Алгоритъм на симплексния методвключва следните стъпки:
- Изготвяне на първия основен план. Преминаване към каноничната форма на задача за линейно програмиране чрез въвеждане на неотрицателни допълнителни балансови променливи.
- Проверка на плана за оптималност. Ако има поне един индексен ред коефициент по-малък от нула, тогава планът не е оптимален и трябва да бъде подобрен.
- Дефиниране на водещи колони и редове. От отрицателните коефициенти на индексната линия се избира най-големият по абсолютна стойност. След това разделя елементите на колоната от свободни членове на симплексната таблица на елементи със същия знак на водещата колона.
- Изграждане на нова базова линия. Преходът към нов план се извършва в резултат на преизчисляване на симплексната таблица по метода на Йордан-Гаус.
Ако е необходимо да се намери екстремумът на целевата функция, тогава говорим за намиране на минималната стойност (F(x) → min , вижте примера за решаване на минимизирането на функцията) и максималната стойност (F(x) → max , вижте примера за решаване на максимизирането на функцията)
Екстремално решение се достига на границата на областта на възможните решения в един от върховете на ъгловите точки на многоъгълника или на отсечката между две съседни ъглови точки.
Основна теорема на линейното програмиране. Ако целевата функция на LLP достигне екстремна стойност в даден момент в областта на възможните решения, тогава тя приема тази стойност в ъгловата точка. Ако целевата функция LLP достигне екстремна стойност в повече от една ъглова точка, тогава тя приема същата стойност във всяка от изпъкналите линейни комбинации на тези точки.
Същността на симплексния метод. Придвижването до оптималната точка се извършва чрез преместване от една ъглова точка към следващата, което приближава и по-бързо до X opt. Такава схема за изброяване на точки, наречен симплексен метод, предложен от Р. Данциг.
Ъгловите точки се характеризират с m основни променливи, така че преходът от една ъглова точка към съседна може да се извърши чрез промяна на само една основна променлива в основата на променлива от небазисната.
Изпълнението на симплексния метод, поради различни характеристики и формулировки на LP проблеми, има различни модификации.
Конструирането на симплексни таблици продължава до получаване на оптималното решение.
Как да използваме симплексна таблица, за да определим, че решението на задача за линейно програмиране е оптимално?
Ако последният ред (стойности на обективната функция) не съдържа отрицателни елементи, тогава той ще намери оптималния план.
Забележка 1. Ако една от основните променливи е равна на нула, тогава екстремната точка, съответстваща на такова основно решение, е изродена. Дегенерация възниква, когато има неяснота при избора на водещ ред. Може изобщо да не забележите израждането на проблема, ако изберете друга линия като ориентир. В случай на неяснота, редът с най-нисък индекс трябва да бъде избран, за да се избегне цикъл.
Забележка 2. Нека в някаква крайна точка всички симплексни разлики са неотрицателни D k ³ 0 (k = 1..n+m), т.е. се получава оптималното решение и съществува такъв A k - небазисен вектор, за който D k = 0. Тогава максимумът се достига поне в две точки, т.е. има алтернативен оптимум. Ако въведем тази променлива x k в основата, стойността на целевата функция няма да се промени.
Забележка 3. Решението на двойната задача е в последната симплексна таблица. Последните m компоненти на вектора на симплексните разлики (в колони с балансови променливи) са оптималното решение на двойната задача. Стойностите на целевите функции на директната и двойната задача в оптималните точки са еднакви.
Забележка 4. При решаване на задачата за минимизиране в основата се въвежда вектор с най-голяма положителна симплексна разлика. Освен това се прилага същият алгоритъм като при проблема за максимизиране.
Ако е поставено условието "Необходимо е суровините от тип III да бъдат напълно изразходвани", то съответното условие е равенство.
Аналитично въведение в симплексния метод
Симплексният метод е универсален метод за линеен програмиране.Така че, ако решим LLP в канонична форма, тогава системата на ограниченията е обичайната система от линейни уравнения. При решаване на LP задачи се получават системи от линейни уравнения, които по правило имат безкрайно много решения.
Например, дадена система
Тук броят на уравненията е 2, а броят на неизвестните е 3, има по-малко уравнения. Изразете x 1 и x 2 по отношение на x 3:
Това е общото решение на системата. ако на променливата x 3 са дадени произволни числови стойности, тогава ще намерим конкретни решения на системата. Например, х 3 =1 → х 1 =1 → х 2=6. Имаме (1, 6, 1) - конкретно решение. Нека бъде х 3 =2 → х 1 =-3, х 2 = 1, (-3, 1, 2) е друго конкретно решение. Има безкрайно много такива конкретни решения.
Променливи х 1 и х 2 се наричат основни, и променливата х 3 - не основно, безплатно.
Набор от променливи х 1 и х 2 формира основата: Б (х 1 , х 2). Ако х 3 = 0, тогава полученото конкретно решение (5, 11, 0) се нарича основно решение, съответстващо на основата Б (х 1 , х 2).
Основно решение е решение, съответстващо на нулеви стойности на свободни променливи.
Други променливи могат да се приемат като основни: ( х 1 , х 3) или ( х 2 , х 3).
Как да преминем от една основа Б(х 1 , х 2) на друга основа Б(х 1 , х 3)?
За това имате нужда от променлива х 3 за преобразуване в основно и х 2 - в неосновни, т.е. в уравненията е необходимо х 3 експресно чрез х 2 и заместване в 1-во:

Б(х 1 , х 3), е: (-19/5; 0; 11/5).
Ако сега от основата Б(х 1 , х 3) искаме да отидем до основата Б(х 2 , х 3), тогава
Основно решение, съответстващо на основата Б (х 2 , х 3): (0;19/4; 7/8).
От трите открити основни решения, решението съответства на основата Б (х 1 , х 3) - отрицателен х 1 < 0, нас в ЗЛП интересуют только неотрицательные решения.
Ако LP задача има решение, то то се постига върху множеството от основни неотрицателни решения на системата за ограничения на каноничната форма.
Следователно идеята на симплексния метод се състои в последователен преход от една основа към друга, най-добрата по отношение на стойността на целевата функция.
Пример. Решете проблема с LP.
Функция Ф= х 2 - х 1 → min трябва да се минимизира за дадена система от ограничения:
-2х 1 + х 2 + х 3 = 2
х 1 + х 2 + х 5 = 5
х 1 - 2х 2 + х 4 = 12
х i ≥ 0, и = 1, 5
Тези ограничения могат да се разглеждат като получени от неравенствата и променливите х 3 , х 5 , х 4 - като допълнителни.
Записваме ограниченията, като избираме база от променливите Б{ х 3 , х 4 , х 5 }:

Тази база съответства на основното неотрицателно решение
х 1 = 0, х 2 = 0, х 3 = 2, х 4 = 2, х 5 = 5 или (0, 0, 2, 2, 5).
Сега трябва да изразим Фчрез неосновни променливи, в нашия случай това вече е направено: Ф= х 2 - х 1 .
Проверете дали функцията е достигнала Фминималната му стойност. За това основно решение Ф= 0 - 0 = 0 - стойността на функцията е 0. Но може да се намали, ако х 1 ще се увеличи, тъй като коефициентът във функцията at х 1 е отрицателно. Въпреки това, с увеличение х 1 променливи стойности х 4 , х 5 намаляват (вижте второто и третото равенство на системата на ограниченията). Променлива хВ противен случай 1 не може да се увеличи до повече от 2 х 4 ще стане отрицателно (поради равенството 2), а в противен случай не повече от 5 х 5 - отрицателен. И така, от анализа на равенствата следва, че променливата х 1 може да се увеличи на 2, като в този случай стойността на функцията ще намалее.
Нека преминем към нова база B 2, като въведем променлива х 1 към база вместо това х 4 .
Б 2 {х 1 , х 3 , х 5 }.
Нека изразим тези основни променливи чрез неосновни. За да направим това, първо изразяваме х 1 от второто уравнение и го заменете с останалото, включително функцията. ![]()
Основно решение, съответстващо на основата Б 3 {х 1 , х 2 , х 3 ), се изписва (4, 1, 9, 0, 0) и функцията приема стойността Ф= -3. Имайте предвид, че стойността Фнамалена, т.е. подобрена в сравнение с предишната база.
Разглеждане на формата на целевата функция ![]() , имайте предвид, че за подобряване, т.е. намаляване на стойността Фне е възможно и само х 4 = 0, х 5 = 0 стойност Ф= -3. веднъж х 4 , х 5 стават положителни, стойност Фще се увеличават само, тъй като коефициентите при х 4 , х 5 са положителни. Така че функцията Фдостигна своя оптимум Ф* = -3. Така че най-малката стойност Ф, равно на -3, се постига при х 1 * = 4, х 2 * = 1, х 3 * = 9, х 4 * = 0, х 5 * = 0.
, имайте предвид, че за подобряване, т.е. намаляване на стойността Фне е възможно и само х 4 = 0, х 5 = 0 стойност Ф= -3. веднъж х 4 , х 5 стават положителни, стойност Фще се увеличават само, тъй като коефициентите при х 4 , х 5 са положителни. Така че функцията Фдостигна своя оптимум Ф* = -3. Така че най-малката стойност Ф, равно на -3, се постига при х 1 * = 4, х 2 * = 1, х 3 * = 9, х 4 * = 0, х 5 * = 0.
Този пример демонстрира идеята на метода много ясно: постепенно преминавайки от база към основа, като винаги обръщаме внимание на стойностите на целевата функция, които трябва да се подобрят, стигаме до основа, в която стойността на целевата функция не може да се подобри, оптимално е. Имайте предвид, че има краен брой бази, така че броят на стъпките, които правим, за да стигнем до желаната база, е краен.
. Алгоритъм на симплексния метод
Пример 5.1.Решете следния проблем за линейно програмиране, като използвате симплексния метод:
решение:
аз повторение:

x3, x4, x5, x6 x1,x2. Ние изразяваме основните променливи по отношение на свободните:

Привеждаме целевата функция до следния вид:
Въз основа на получения проблем ще формираме началната симплексна таблица:
Таблица 5.3
Първоначална симплексна таблица
Прогнозни отношения |
||||
Според дефиницията на основното решение, свободните променливи са равни на нула, а стойностите на основните променливи са равни на съответните стойности на свободните числа, т.е.
Етап 3: проверка на съвместимостта на системата от ограничения на LLP.
При тази итерация (в Таблица 5.3) знакът за несъответствие на системата за ограничения (характеристика 1) не беше разкрит (т.е. няма ред с отрицателно свободно число (с изключение на линията на целевата функция), която не съдържа най-малко един отрицателен елемент (т.е. отрицателен коефициент за свободна променлива)).
При тази итерация (в таблица 5.3) знакът за неограниченост на целевата функция (знак 2) не беше разкрит (т.е. няма колона с отрицателен елемент в реда на целевата функция (с изключение на колоната със свободни числа) в който би имало поне един положителен елемент) .
Тъй като намереното основно решение не съдържа отрицателни компоненти, то е допустимо.
Етап 6: проверка на оптималността.
Намереното основно решение не е оптимално, тъй като според критерия за оптималност (знак 4) в реда на целевата функция не трябва да има отрицателни елементи (свободният номер на тази линия не се взема предвид при разглеждането на този знак ). Следователно, според алгоритъма на симплексния метод, преминаваме към 8-ми етап.
Тъй като намереното основно решение е допустимо, ще търсим разделящата колона по следната схема: определяме колоните с отрицателни елементи в реда на целевата функция (с изключение на колоната със свободни числа). Според таблица 5.3 има две такива колони: колоната " x1" и колона " x2". От такива колони се избира тази, която съдържа най-малкия елемент в реда на целевата функция. Тя ще се реши. говорител" x2' съдържа най-малкия елемент (-3) в сравнение с колоната ' x1
За да определим разрешителния низ, намираме положителните изчислени съотношения на свободните числа към елементите на разрешителната колона, низът, който съответства на най-малкото положително изчислено съотношение, се приема като разрешен.
Таблица 5.4
Първоначална симплексна таблица
В таблица 5.4 най-малкото положително съотношение на оценка съответства на реда " x5“, следователно, то ще бъде разрешаващо.
Елементът, разположен в пресечната точка на разрешаващата колона и разрешаващата линия, се приема като разрешаващ. В нашия пример това е елементът, който се намира в пресечната точка на линията " x5» и колони « x2».
Разделящият елемент показва една основна и една свободна променливи, които трябва да бъдат разменени в симплексната таблица, за да се премине към новото „подобрено“ основно решение. В този случай това са променливи. x5и x2, в новата симплексна таблица (таблица 5.5) ги разменяме.
9.1. Разрешаване на трансформация на елемент.
Разрешителният елемент от таблица 5.4 се трансформира, както следва:
![]()
Въвеждаме получения резултат в подобна клетка в таблица 5.5.
9.2. Разрешаване на преобразуване на низове.
Елементите на разрешителната линия на таблица 5.4 са разделени на разрешителния елемент на тази симплексна таблица, резултатите се вписват в подобни клетки на новата симплексна таблица (таблица 5.5). Трансформациите на елементите на разрешаващия низ са дадени в Таблица 5.5.
9.3. Разрешителна трансформация на колона.
Елементите на разделителната колона от таблица 5.4 се разделят на разделящия елемент на тази симплексна таблица и резултатът се взема с противоположен знак. Получените резултати се вписват в подобни клетки на новата симплексна таблица (таблици 5.5). Трансформациите на елементи от разделителната колона са дадени в Таблица 5.5.
9.4. Преобразуване на останалите елементи от симплексната таблица.
Преобразуването на други елементи от симплексната таблица (т.е. елементи, които не са разположени в разделящия ред и разделящата колона) се извършва съгласно правилото "правоъгълник".
Например, помислете за трансформацията на елемент, разположен в пресечната точка на низа " x3” и колони „”, условно го обозначават като „ x3". В таблица 5.4 мислено начертаваме правоъгълник, единият връх на който се намира в клетката, чиято стойност се трансформира (т.е. в клетката " x3”), а другият (диагонален връх) е в клетка с разделящ елемент. Другите два върха (на втория диагонал) са еднозначно определени. Тогава трансформираната стойност на клетката " x3"ще бъде равна на предишната стойност на тази клетка минус дроб, в знаменателя на която е разделящият елемент (от таблица 5.4), а в числителя продуктът на два други неизползвани върха, т.е.:
« x3»: .
Стойностите на други клетки се преобразуват по подобен начин:
« x3 x1»: ;
« x4»: ![]() ;
;
« x4 x1»: ;
« x6»: ![]() ;
;
« x6 x1»: ;
«»: ![]() ;
;
« x1»: ![]() .
.
В резултат на тези трансформации е получена нова симплексна таблица (таблица 5.5).
II повторение:
Етап 1: съставяне на симплексна таблица.
Таблица 5.5
Симплексна масаII итерации
Изчислено отношения |
||||
| ||||
|
|
Етап 2: определяне на основното решение.
В резултат на симплексните трансформации се получава ново основно решение (таблица 5.5):
Както можете да видите, с това основно решение стойността на целевата функция =15, което е повече, отколкото при предишното основно решение.
Не е установено несъответствие на системата от ограничения в съответствие със знак 1 в таблица 5.5.
Етап 4: проверка на ограничеността на целевата функция.
Неограничеността на целевата функция в съответствие със знак 2 в Таблица 5.5 не беше разкрита.
Етап 5: проверка на допустимостта на намереното основно решение.
Намереното основно решение в съответствие с характеристика 4 не е оптимално, тъй като реда на целевата функция на симплексната таблица (Таблица 5.5) съдържа отрицателен елемент: -2 (свободният номер на този ред не се взема предвид при разглеждането на това отличителен белег). Така че нека преминем към стъпка 8.
Етап 8: дефиниране на активиращия елемент.
8.1. Определение на колона за разделителна способност.
Намереното основно решение е допустимо, определяме колоните с отрицателни елементи в реда на целевата функция (с изключение на колоната със свободни числа). Според таблица 5.5 има само една такава колона: " x1". Следователно ние го приемаме като разрешено.
8.2. Разрешителна дефиниция на низ.
Според получените стойности на положителните изчислени съотношения в таблица 5.6, минимумът е съотношението, съответстващо на реда " x3". Следователно ние го приемаме като разрешено.
Таблица 5.6
Симплексна масаII итерации
Изчислено отношения |
||||
3/1=3 – мин |
||||
Етап 9: трансформация на симплексната таблица.
Трансформациите на симплексната таблица (Таблица 5.6) се извършват по същия начин, както в предишната итерация. Резултатите от трансформациите на елементи от симплексната таблица са показани в Таблица 5.7.
III повторение
Въз основа на резултатите от симплексните трансформации от предишната итерация, ние съставяме нова симплексна таблица:
Таблица 5.7
Симплексна масаIII итерации
Изчислено отношения |
||||
| ||||
|
|
Етап 2: определяне на основното решение.
В резултат на симплексните трансформации се получава ново основно решение (таблица 5.7):
Етап 3: проверка на съвместимостта на системата от ограничения.
Не е установено несъответствие на системата от ограничения в съответствие със знак 1 в таблица 5.7.
Етап 4: проверка на ограничеността на целевата функция.
Неограничеността на целевата функция в съответствие със знак 2 в таблица 5.7 не беше разкрита.
Етап 5: проверка на допустимостта на намереното основно решение.
Намереното основно решение по критерий 3 е допустимо, тъй като не съдържа отрицателни компоненти.
Етап 6: проверка на оптималността на намереното основно решение.
Намереното основно решение в съответствие с характеристика 4 не е оптимално, тъй като редът на целевата функция на симплексната таблица (Таблица 5.7) съдържа отрицателен елемент: -3 (свободният номер на този ред не се взема предвид при разглеждането на това отличителен белег). Така че нека преминем към стъпка 8.
Етап 8: дефиниране на активиращия елемент.
8.1. Определение на колона за разделителна способност.
Намереното основно решение е допустимо, определяме колоните с отрицателни елементи в реда на целевата функция (с изключение на колоната със свободни числа). Според таблица 5.7 има само една такава колона: " x5". Следователно ние го приемаме като разрешено.
8.2. Разрешителна дефиниция на низ.
Според получените стойности на положителните изчислени съотношения в таблица 5.8, минимумът е съотношението, съответстващо на реда " x4". Следователно ние го приемаме като разрешено.
Таблица 5.8
Симплексна масаIII итерации
Изчислено отношения |
||||
5/5=1 – мин |
||||
Етап 9: трансформация на симплексната таблица.
Трансформациите на симплексната таблица (Таблица 5.8) се извършват по същия начин, както в предишната итерация. Резултатите от трансформациите на елементите на симплексната таблица са показани в Таблица 5.9.
IV повторение
Етап 1: изграждане на нова симплексна маса.
Въз основа на резултатите от симплексните трансформации от предишната итерация, ние съставяме нова симплексна таблица:
Таблица 5.9
Симплексна масаIV итерации
Изчислено отношения |
||||
| –(–3/5)=3/5 | |||
–(1/5)=–1/5 | ||||
| –(9/5)=–9/5 | |||
|
| –(–3/5)=3/5 |
Етап 2: определяне на основното решение.
В резултат на симплексните трансформации е получено ново основно решение, съгласно таблица 5.9, решението е както следва:
Етап 3: проверка на съвместимостта на системата от ограничения.
Не е разкрита несъответствие на системата от ограничения в съответствие с характеристика 1 в таблица 5.9.
Етап 4: проверка на ограничеността на целевата функция.
Неограничеността на целевата функция в съответствие със знак 2 в таблица 5.9 не беше разкрита.
Етап 5: проверка на допустимостта на намереното основно решение.
Намереното основно решение по критерий 3 е допустимо, тъй като не съдържа отрицателни компоненти.
Етап 6: проверка на оптималността на намереното основно решение.
Основното решение, намерено в съответствие с характеристика 4, е оптимално, тъй като няма отрицателни елементи в реда на целевата функция на симплексната таблица (Таблица 5.9) (свободният номер на този ред не се взема предвид при разглеждането на тази характеристика) .
Етап 7: проверка на алтернативното решение.
Намереното решение е единственото, тъй като в реда на целевата функция няма нулеви елементи (Таблица 5.9) (свободният номер на тази линия не се взема предвид при разглеждането на тази характеристика).
Отговор: оптималната стойност на целевата функция на разглежданата задача =24, която се постига при.
Пример 5.2.Решете горния проблем за линейно програмиране, като приемете, че целевата функция е минимизирана:
решение:
аз повторение:
Етап 1: формиране на първоначалната симплексна таблица.
Оригиналната задача за линейно програмиране е дадена в стандартна форма. Нека го приведем до канонична форма, като във всяко от ограниченията на неравенството въведем допълнителна неотрицателна променлива, т.е.

В получената система от уравнения приемаме като разрешени (основни) променливи x3, x4, x5, x6, то свободните променливи са x1,x2. Изразяваме основните променливи чрез свободните.
Ако трябва да решите задача за линейно програмиране с помощта на симплексни таблици, тогава нашата онлайн услуга ще ви бъде от голяма помощ. Симплексният метод предполага последователно изброяване на всички върхове от областта на допустимите стойности, за да се намери върхът, където функцията придобива екстремна стойност. На първия етап се намира някакво решение, което се подобрява на всяка следваща стъпка. Такова решение се нарича основно. Ето последователност от действия при решаване на задача за линейно програмиране с помощта на симплексния метод:
Първа стъпка. В съставената таблица първо трябва да погледнете колоната със свободни членове. Ако съдържа отрицателни елементи, тогава е необходимо да се премине към втората стъпка, ако не, тогава към петата.
Втора стъпка. На втората стъпка е необходимо да се реши коя променлива да се изключи от базата и коя да се включи, за да се преизчисли симплексната таблица. За да направите това, разглеждаме колоната със свободни членове и намираме отрицателен елемент в нея. Ред с отрицателен елемент ще се нарича водещ. В него намираме максималния отрицателен елемент в абсолютна стойност, колоната, съответстваща на него, е последователят. Ако има отрицателни стойности сред свободните членове, но не и в съответния ред, тогава такава таблица няма да има решения. Променливата във водещия ред, която е в колоната със свободни членове, се изключва от базата, а променливата, съответстваща на водещата колона, се включва в базата.
Маса 1.
| базисни променливи | Безплатни членове в ограничения | Неосновни променливи | |||||
| х 1 | x2 | ... | х л | ... | x n | ||
| xn+1 | б 1 | а 11 | а 12 | ... | а 1л | ... | a 1n |
| xn+2 | б 2 | а 21 | а 22 | ... | а 2л | ... | a 2n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| xn+r | b2 | a r1 | a r2 | ... | a rl | ... | a rn |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| xn+m | б м | a m1 | един m2 | ... | aml | ... | amn |
| F(x)макс | F0 | -c 1 | -c 2 | ... | -c 1 | ... | -c n |
Трета стъпка. На третата стъпка преизчисляваме цялата симплексна таблица с помощта на специални формули, тези формули могат да се видят с помощта на .
Четвърта стъпка. Ако след преизчисление в колоната със свободни членове останат отрицателни елементи, преминете към първата стъпка, ако няма такива, преминете към петата.
Пета стъпка. Ако сте стигнали до петата стъпка, значи сте намерили решение, което е приемливо. Това обаче не означава, че е оптимално. Ще бъде оптимално само ако всички елементи в F-реда са положителни. Ако това не е така, тогава е необходимо да се подобри решението, за което намираме водещия ред и колона за следващо преизчисление по следния алгоритъм. Първоначално намираме минималното отрицателно число в ред F, с изключение на стойността на функцията. Колоната с това число ще бъде водеща. За да намерим водещия ред, намираме съотношението на съответния свободен член и елемента от водещата колона, при условие че са положителни. Минималното съотношение ще определи водещата линия. Преизчисляваме таблицата според формулите, т.е. преминете към стъпка 3.
Намерете най-голямата стойност на функция
x 1 ≥ 0 x 2 ≥ 01. Свободните членове на системата трябва да са неотрицателни.
Това условие е изпълнено.
2. Всяко ограничение на системата трябва да бъде уравнение.
| х 1 + | 2 | x2 | ≤ | 4 | ||
| х 1 | - | x2 | ≥ | 1 | ||
| х 1 | + | x2 | ≤ | 8 |
| х 1 + | 2 | x2 | + | S1 | = | 4 | |||||||||
| х 1 | - | x2 | - | S2 | = | 1 | |||||||||
| х 1 | + | x2 | + | S3 | = | 8 |
S 1 ≥ 0, S 2 ≥ 0, S 3 ≥ 0. Въведените променливи S 1 , S 2 , S 3 се наричат балансови променливи.
3. Намиране на началната база и стойността на функцията F, която съответства на намерената начална база.
Какво е основа?
Променлива се нарича основна за дадено уравнение, ако влиза в даденото уравнение с фактор еднои не се включва в останалите уравнения на системата (при условие, че има неотрицателно число от дясната страна на уравнението).
Ако всяко уравнение има базисна променлива, тогава се казва, че системата има основа.
Променливите, които не са основни, се наричат свободни променливи.
Каква е идеята зад симплексния метод?
Всяка база съответства на една стойност на функцията. Една от тях е най-голямата стойност на функцията F.
Ще преминем от една основа към друга.
Следващата база ще бъде избрана по такъв начин, че да се получи стойността на функцията F не по-малка от съществуващата.
Очевидно броят на възможните бази за всеки проблем не е много голям.
Следователно рано или късно отговорът ще бъде получен.
Как се осъществява преходът от една основа към друга?
По-удобно е решението да се записва под формата на таблици. Всеки ред от таблицата е еквивалентен на уравнението на системата. Маркираният ред се състои от коефициентите на функцията (вижте таблицата по-долу). Това ви позволява да не пренаписвате променливи всеки път, което спестява много време.
В избрания ред изберете най-големия положителен коефициент (можете да изберете всеки положителен).
Това е необходимо, за да се получи стойността на функцията F не по-малка от съществуващата.
Избрана е колона.
За положителни коефициенти на избраната колона изчисляваме съотношението Θ и избираме най-малката стойност.
Това е необходимо, за да може след трансформацията колоната със свободни членове да остане неотрицателна.
Редът е избран.
Елементът, който ще бъде основен елемент, е дефиниран. След това броим.
Нашата система има ли основа?
| х 1 + | 2 | x2 | + | S1 | = | 4 | |||||||||
| х 1 | - | x2 | - | S2 | = | 1 | |||||||||
| х 1 | + | x2 | + | S3 | = | 8 |
Няма основание, т.е. не можем да започнем решение.
Ще трябва да го намеря. За да направим това, решаваме спомагателна задача.
Нека добавим изкуствена променлива към уравнението, където няма основна променлива.
| х 1 + | 2 | x2 | + | S1 | = | 4 | ||||||||||||
| х 1 | - | x2 | - | S2 | + | R1 | = | 1 | ||||||||||
| х 1 | + | x2 | + | S3 | = | 8 |
R 1 ≥ 0. Въведената променлива R 1 се нарича изкуствена променлива.
Въвеждаме под внимание функцията W и търсим нейната най-малка стойност.
Алгоритъмът за намиране на най-малката стойност на функцията W има само една разлика от алгоритъма, разгледан по-горе.
| х 1 | x2 | S1 | S2 | S3 | R1 | Св. член | Θ |
| 1 | 2 | 1 | 0 | 0 | 0 | 4 | 4: 1 = 4 |
| 1 | -1 | 0 | -1 | 0 | 1 | 1 | 1: 1 = 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 8 | 8: 1 = 8 |
| -1 | 1 | 0 | 1 | 0 | 0 | W - 1 | |
| 0 | 3 | 1 | 1 | 0 | -1 | 3 | |
| 1 | -1 | 0 | -1 | 0 | 1 | 1 | |
| 0 | 2 | 0 | 1 | 1 | -1 | 7 | |
| 0 | 0 | 0 | 0 | 0 | 1 | W - 0 |
Приравняваме свободните променливи към нула. Намерете устно стойностите на основните променливи. (виж таблицата)
Функцията W се изразява чрез свободни променливи. Следователно стойността на функцията W за дадена база може да бъде намерена незабавно. (виж маркирания ред на таблицата)
| x 2 = 0 S 2 = 0 R 1 = 0 x 1 = 1 S 1 = 3 S 3 = 7 |
=> W - 0 = 0 => W = 0 |
Сред коефициентите на избрания ред няма отрицателни. Следователно се намира най-малката стойност на функцията W.
Получава се база без използване на изкуствена променлива. Което се изискваше.
Колоната, съответстваща на изкуствената променлива, може да бъде зачертана.
В резултат на това нашата система изглежда така:
| 3 | x2 | + | S1 | + | S2 | = | 3 | |||||||||
| х 1 | - | x2 | - | S2 | = | 1 | ||||||||||
| 2 | x2 | + | S2 | + | S3 | = | 7 |
| Ф | = | - | х 1 | + | 3 | x2 |
|
|